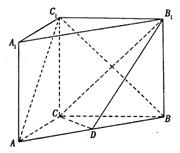
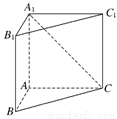
摘要:19. 在直三棱柱ABC-A1B1C1中.A1A=AB=3.AC=3.∠CAB=90°.P.Q分别为棱BB1.CC1上的点.且BP=BB1.CQ=CC1. (1)求平面APQ与面ABC所成的锐二面角的大小. (2)在线段A1B上是否存在一点M.使AM+MC1最小?若存在.求出最小值,若不存在.说明理由. [解析](1)建立如图所示空间直角坐标系A-xyz. A.P(3.0.).Q(0.3.2). =(3.0.).=(0.3.2). 设平面APQ的一个法向量为n1=(x,y,z) 令z=3.则x=-1.y=-2.∴n1=(-1.-2.3) 平面ABC的一个法向量n2=. ∴cos〈n1.n2〉= ∴平面APQ与面ABC所成的锐角大小为45°. (1)问也可用传统方法求解. (2)沿A1B将面A1BC1与面A1BA展开.连结AC1与A1B交于点M.此时AM+MC1有最小值. ∵∠A1AB=90°.AA1=AB.∴∠A1AB=45°.又C1A1⊥面ABB1A1.∴C1A1⊥A1B. ∴△AA1C1中.∠AA1C1=135° AC1=, ∴存在点M.使AM+MC1取最小值为3.
网址:http://m.1010jiajiao.com/timu_id_4045147[举报]
.(本小题满分12分)
如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点,
(I)求证: AC 1//平面CDB1;
(II)求二面角C1-AB-C的平面角的正切值。

查看习题详情和答案>>
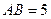 ,AA1=3,点D是AB的中点.
,AA1=3,点D是AB的中点.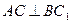
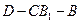 的大小.
的大小.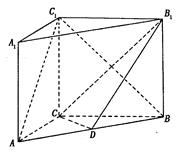
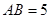 ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.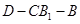 的平面角的正切值.
的平面角的正切值.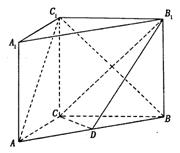
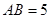 ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.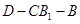 的余弦值.
的余弦值.