摘要:16. 如图.四面体ABCD中.O是BD的中点.ΔABD和ΔBCD均为等边三角形. AB =2 , AC =. (I)求证:平面BCD, (II)求二面角A-BC- D的大小, (III)求O点到平面ACD的距离.
网址:http://m.1010jiajiao.com/timu_id_4044573[举报]
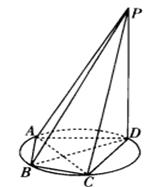 (本小题满分14分)如图5 所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径, ∠ABD=60o,∠BDC=45o.△ADP∽△BAD.
(本小题满分14分)如图5 所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径, ∠ABD=60o,∠BDC=45o.△ADP∽△BAD.
(1)求线段PD的长;
(2)若![]() ,求三棱锥P-ABC的体积.
,求三棱锥P-ABC的体积.
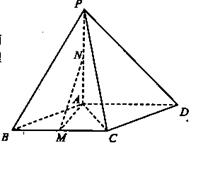
(本小题满分14分)
如图:在四棱锥![]() 中,底面ABCD是菱形,
中,底面ABCD是菱形,![]() ,
,![]() 平面ABCD,点M,N分别为BC,PA的中
平面ABCD,点M,N分别为BC,PA的中![]() 点,且
点,且![]()
(I)证明:![]() 平面AMN;
平面AMN;
(II)求三棱锥N![]() 的体积;
的体积;
(III)在线段PD上是否存在一点E,![]() 使得
使得![]() 平面ACE;若存在,求出PE的长,若不存在,说明理由。
平面ACE;若存在,求出PE的长,若不存在,说明理由。
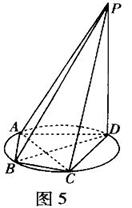
(本小题满分14分)如图5所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,![]() 。
。
(1)求线段PD的长;
(2)若![]() ,求三棱锥P-ABC的体积。
,求三棱锥P-ABC的体积。
 .
.
