摘要:(1)空间向量的坐标:空间直角坐标系的x轴是横轴.y轴是纵轴.z轴是竖轴. ①令=(a1,a2,a3),.则 ∥ (用到常用的向量模与向量之间的转化:) ②空间两点的距离公式:. (2)法向量:若向量所在直线垂直于平面.则称这个向量垂直于平面.记作.如果那么向量叫做平面的法向量. (3)用向量的常用方法: ①利用法向量求点到面的距离定理:如图.设n是平面的法向量.AB是平面的一条射线.其中.则点B到平面的距离为. ②利用法向量求二面角的平面角定理:设分别是二面角中平面的法向量.则所成的角就是所求二面角的平面角或其补角大小(方向相同.则为补角.反方.则为其夹角). ③证直线和平面平行定理:已知直线平面..且CDE三点不共线.则a∥的充要条件是存在有序实数对使.(常设求解若存在即证毕.若不存在.则直线AB与平面相交).
网址:http://m.1010jiajiao.com/timu_id_4044472[举报]
在空间直角坐标系O-xyz中,
=x
+y
+z
(其中
,
,
分别为x轴、y轴、z轴正方向上的单位向量).有下列命题:
①若
=x
+y
+0
(x>0,y>0)且|
-4
|=|
+2
|,则
+
的最小值为2
②若
=0
+y
+z
,
=0
+y1
+
,若向量
与
共线且|
|=|
|,则动点P的轨迹是抛物线;
③若
=a
+0
+0
,
=0
+b
+0
,
=0
+0
+c
(abc≠0),则平面MQR内的任意一点A(x,y,z)的坐标必须满足关系式
+
+
=1;
④设
=x
+y
+0
(x∈[0,4],y∈[-4,4]),
=0
+y1
+
(y1∈[-4,4]),
=x2
+0
+0
(x2∈[0,4]),若向量
⊥
,
与
共线且|
|=|
|,则动点P的轨迹是双曲线的一部分.
其中你认为正确的所有命题的序号为
查看习题详情和答案>>
| OP |
| i |
| j |
| k |
| i |
| j |
| k |
①若
| OP |
| i |
| j |
| k |
| OP |
| j |
| OP |
| i |
| 1 |
| x |
| 2 |
| y |
| 2 |
②若
| OP |
| i |
| j |
| k |
| OQ |
| i |
| j |
| k |
| PQ |
| k |
| PQ |
| OP |
③若
| OM |
| i |
| j |
| k |
| OQ |
| i |
| j |
| k |
| OR |
| i |
| j |
| k |
| x |
| a |
| y |
| b |
| z |
| c |
④设
| OP |
| i |
| j |
| k |
| OM |
| i |
| j |
| k |
| ON |
| i |
| j |
| k |
| PM |
| j |
| PN |
| j |
| PM |
| PN |
其中你认为正确的所有命题的序号为
②③④
②③④
.在空间直角坐标系O-xyz中,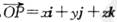 (其中i、j、k分别为X轴、y轴、z轴正方向上的单位向量).有下列命题:
(其中i、j、k分别为X轴、y轴、z轴正方向上的单位向量).有下列命题:
①若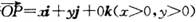 且
且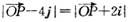 ,则
,则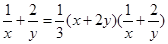
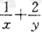 的最小值为
的最小值为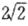 ;
;
②设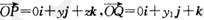 ,若向量
,若向量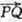 与k共线且
与k共线且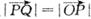 ,则动点P的轨迹是抛物线;
,则动点P的轨迹是抛物线;
③若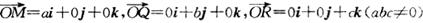 ,则平面MQR内的任意一点A (x,y,z)的坐标必然满足关系式
,则平面MQR内的任意一点A (x,y,z)的坐标必然满足关系式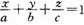 ;
;
④设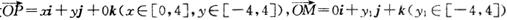 ,
,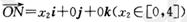 ,若向量
,若向量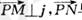 与j共线且
与j共线且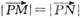 ,则动点P的轨迹是双曲线的一部分.
其中你认为正确的所有命题的序号为. _______
,则动点P的轨迹是双曲线的一部分.
其中你认为正确的所有命题的序号为. _______
查看习题详情和答案>>
在空间直角坐标系中,对其中任何一向量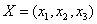 ,定义范数
,定义范数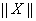 ,它满足以下性质:
,它满足以下性质:
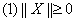 ,当且仅当
,当且仅当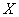 为零向量时,不等式取等号;
为零向量时,不等式取等号;
(2)对任意的实数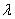 ,
,
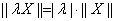 (注:此处点乘号为普通的乘号);
(注:此处点乘号为普通的乘号);
(3)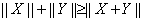 ;
;
试求解以下问题:在平面直角坐标系中,有向量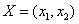 ,下面给出的几个表达式中,可能表示向量
,下面给出的几个表达式中,可能表示向量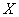 的范数的是____(把所有正确答案的序号都填上).
的范数的是____(把所有正确答案的序号都填上).
(1)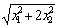 (2)
(2)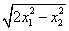 (3)
(3)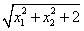 (4)
(4)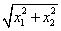
查看习题详情和答案>>
 如图,空间直角坐标系O-xyz中,已知A(1,0,0),B(0,2,0),现将△AOB按向量
如图,空间直角坐标系O-xyz中,已知A(1,0,0),B(0,2,0),现将△AOB按向量