摘要:[例1]求过点(0.2)的直线被椭圆x2+2y2=2所截弦的中点的轨迹方程. 解:设直线方程为y=kx+2. 把它代入x2+2y2=2. 整理得(2k2+1)x2+8kx+6=0. 要使直线和椭圆有两个不同交点.则Δ>0.即k<-或k>. 设直线与椭圆两个交点为A(x1.y1).B(x2.y2).中点坐标为C(x.y).则 x==. y= +2=. (k<-或k>). 从参数方程 x=. y= 消去k得x2+2(y-1)2=2. 且|x|<.0<y<. [例2] 如图.M是抛物线上y2=x上的一点.动弦ME.MF分别交x轴于A.B两点.且MA=MB. (1)若M为定点.证明:直线EF的斜率为定值, (2)若M为动点.且∠EMF=90°.求△EMF的重心G的轨迹方程. 解:(1)设M(y,y0).直线ME的斜率为k(l>0) 则直线MF的斜率为-k. 消 所以直线EF的斜率为定值 (2) 同理可得 设重心G(x, y).则有 [例3]如图.椭圆=1(a>b>0)与过点A(2.0)B(0,1)的直线有且只有一个公共点T.且椭圆的离心率e=. (Ⅰ)求椭圆方程, (Ⅱ)设F.F分别为椭圆的左.右焦点.M为线段的中点.求证:∠ATM=∠AFT. 解:(I)过点.的直线方程为 因为由题意得 有惟一解. 即有惟一解. 所以 (). 故 又因为 即 所以 从而得 故所求的椭圆方程为 (II)由(I)得 故 从而 由 解得所以 因为 又得 因此 [例4]已知椭圆C:+=1(a>b>0).两个焦点分别为F1和F2.斜率为k的直线l过右焦点F2且与椭圆交于A.B两点.设l与y轴交点为P.线段PF2的中点恰为B. (1)若|k|≤.求椭圆C的离心率的取值范围, (2)若k=.A.B到右准线距离之和为.求椭圆C的方程. 解:(1)设右焦点F2(c.0).则l:y=k(x-c). 令x=0.则y=-ck.∴P(0.-ck). ∵B为F2P的中点.∴B(.-). ∵B在椭圆上.∴+=1. ∴k2=·=(-1)(4-e2) =+e2-5. ∵|k|≤.∴+e2-5≤. ∴(5e2-4)(e2-5)≤0. ∴≤e2<1.∴≤e<1. (2)k=.∴e=.∴=. ∴a2=c2.b2=c2.椭圆方程为+=1.即x2+5y2=c2. 直线l方程为y=(x-c). B(.-c).右准线为x=c. 设A(x0.y0).则 (c-x0)+(c-)=. ∴x0=2c-.y0=(c-). ∵A在椭圆上. ∴(2c-)2+5[(c-)]2=c2. 解之得c=2或c=. ∴椭圆方程为x2+5y2=5.即+y2=1. [研讨.欣赏]双曲线C与椭圆有相同的焦点.直线为C的一条渐近线. (1)求双曲线C的方程, (2)过点的直线.交双曲线C于A.B两点.交轴于Q点(Q点与C的顶点不重合).当.且时.求点的坐标. 解:(Ⅰ)设双曲线方程为 由椭圆 求得两焦点为. 对于双曲线.又为双曲线的一条渐近线 解得 . 双曲线的方程为 (Ⅱ)解法一: 由题意知直线的斜率存在且不等于零. 设的方程:. 则 在双曲线上. 同理有: 若则直线过顶点.不合题意. 是二次方程的两根. . 此时. 所求的坐标为. 解法二: 由题意知直线的斜率存在且不等于零 设的方程..则. . 分的比为. 由定比分点坐标公式得 下同解法一 解法三: 由题意知直线的斜率存在且不等于零 设的方程:.则. . . . .. 又. 即 将代入得 .否则与渐近线平行. . 解法四: 由题意知直线l得斜率k存在且不等于零.设的方程:. 则 , . 同理 . 即 . (*) 又 消去y得. 当时.则直线l与双曲线得渐近线平行.不合题意.. 由韦达定理有: 代入(*)式得 所求Q点的坐标为.
网址:http://m.1010jiajiao.com/timu_id_4044419[举报]
(2012•汕头二模)已知平面内一动点 P到定点F(0,
)的距离等于它到定直线y=-
的距离,又已知点 O(0,0),M(0,1).
(1)求动点 P的轨迹C的方程;
(2)当点 P(x0,y0)(x0≠0)在(1)中的轨迹C上运动时,以 M P为直径作圆,求该圆截直线y=
所得的弦长;
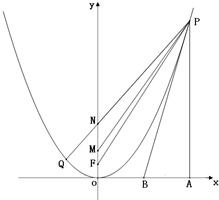
(3)当点 P(x0,y0)(x0≠0)在(1)中的轨迹C上运动时,过点 P作x轴的垂线交x轴于点 A,过点 P作(1)中的轨迹C的切线l交x轴于点 B,问:是否总有 P B平分∠A PF?如果有,请给予证明;如果没有,请举出反例.
查看习题详情和答案>>
| 1 |
| 2 |
| 1 |
| 2 |
(1)求动点 P的轨迹C的方程;
(2)当点 P(x0,y0)(x0≠0)在(1)中的轨迹C上运动时,以 M P为直径作圆,求该圆截直线y=
| 1 |
| 2 |
(3)当点 P(x0,y0)(x0≠0)在(1)中的轨迹C上运动时,过点 P作x轴的垂线交x轴于点 A,过点 P作(1)中的轨迹C的切线l交x轴于点 B,问:是否总有 P B平分∠A PF?如果有,请给予证明;如果没有,请举出反例.
已知点P是直角坐标平面内的动点,点P到直线l1:x=-2的距离为d1,到点F(-1,0)的距离为d2,且
=
.
(1)求动点P所在曲线C的方程;
(2)直线l过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线l1:x=-2的垂线,对应的垂足分别为M、N,试判断点F与以线段MN为直径的圆的位置关系(指在圆内、圆上、圆外等情况);
(3)记S1=S△FAM,S2=S△FMN,S3=S△FBN(A、B、M、N是(2)中的点),问是否存在实数λ,使S22=λS1S3成立.若存在,求出λ的值;若不存在,请说明理由.
进一步思考问题:若上述问题中直线l1:x=-
、点F(-c,0)、曲线C:
+
=1(a>b>0,c=
),则使等式S22=λS1S3成立的λ的值仍保持不变.请给出你的判断 (填写“不正确”或“正确”)(限于时间,这里不需要举反例,或证明).
查看习题详情和答案>>
| d2 |
| d1 |
| ||
| 2 |
(1)求动点P所在曲线C的方程;
(2)直线l过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线l1:x=-2的垂线,对应的垂足分别为M、N,试判断点F与以线段MN为直径的圆的位置关系(指在圆内、圆上、圆外等情况);
(3)记S1=S△FAM,S2=S△FMN,S3=S△FBN(A、B、M、N是(2)中的点),问是否存在实数λ,使S22=λS1S3成立.若存在,求出λ的值;若不存在,请说明理由.
进一步思考问题:若上述问题中直线l1:x=-
| a2 |
| c |
| x2 |
| a2 |
| y2 |
| b2 |
| a2-b2 |
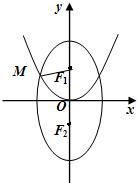 与向量、圆交汇.例5:已知F1、F2分别为椭圆C1:
与向量、圆交汇.例5:已知F1、F2分别为椭圆C1:| y2 |
| a2 |
| x2 |
| b2 |
| 5 |
| 3 |
(1)求椭圆C1的方程;
(2)已知点P(1,3)和圆O:x2+y2=b2,过点P的动直线l与圆O相交于不同的两点A,B,在线段AB上取一点Q,满足:
| AP |
| PB |
| AQ |
| QB |
 已知四点O(0,0),
已知四点O(0,0),