摘要：13．正棱锥:底面是正多边形.顶点在底面上的射影是底面的中心的棱锥叫正棱锥．(1)正棱锥的各侧棱相等.各侧面是全等的等腰三角形.各等腰三角形底边上的高相等正棱锥的高.斜高.斜高在底面上的射影组成一个直角三角形,正棱锥的高.侧棱.侧棱在底面上的射影也组成一个直角三角形
网址：http://m.1010jiajiao.com/timu_id_4042557[举报]
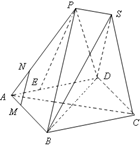已知四边形ABCD为菱形，AB=6，∠BAD=60°，两个正三棱锥P-ABD、S-BCD（底面是正三角形且顶点在底面上的射影是底面正三角形的中心）的侧棱长都相等，如图，E、M、N分别在AD、AB、AP上，且AM=AE=2，AN=
| 1 | 3 |
（Ⅰ）求证：PB⊥平面PAD；
（Ⅱ）求平面BPS与底面ABCD所成锐二面角的平面角的正切
值；
（Ⅲ）求多面体SPABC的体积． 查看习题详情和答案>>
已知四边形ABCD为菱形，AB=6，∠BAD=60°，两个正三棱锥P-ABD、S-BCD（底面是正三角形且顶点在底面上的射影是底面正三角形的中心）的侧棱长都相等，如图，E、M、N分别在AD、
AB、AP上，且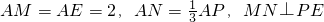
．
（Ⅰ）求证：PB⊥平面PAD；
（Ⅱ）求平面BPS与底面ABCD所成锐二面角的平面角的正切
值；
（Ⅲ）求多面体SPABC的体积．
查看习题详情和答案>>
已知四边形ABCD为菱形，AB=6，∠BAD=60°，两个正三棱锥P-ABD、S-BCD（底面是正三角形且顶点在底面上的射影是底面正三角形的中心）的侧棱长都相等，如图，E、M、N分别在AD、
AB、AP上，且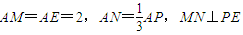
．
（Ⅰ）求证：PB⊥平面PAD；
（Ⅱ）求平面BPS与底面ABCD所成锐二面角的平面角的正切
值；
（Ⅲ）求多面体SPABC的体积．
查看习题详情和答案>>
AB、AP上，且
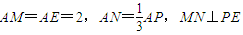．（Ⅰ）求证：PB⊥平面PAD；
（Ⅱ）求平面BPS与底面ABCD所成锐二面角的平面角的正切
值；
（Ⅲ）求多面体SPABC的体积．
查看习题详情和答案>>
．