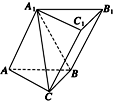
摘要：如图所示.在三棱柱ABC-A1B1C1中.四边形A1ABB1是菱形.四边形BCC1B1是矩形.AB⊥BC.CB=3.AB=4.∠A1AB=60°. (1)求证:平面CA1B⊥平面A1ABB1, (2)求直线A1C与平面BCC1B1所成角的正切值, (3)求点C1到平面A1CB的距离. (1)证明 ∵四边形BCC1B1是矩形.∴BC⊥BB1. 又∵AB⊥BC.∴BC⊥平面A1ABB1. ∵BC平面CA1B.∴平面CA1B⊥平面A1ABB1. (2)解 过A1作A1D⊥B1B于D.连接DC.∵BC⊥平面A1ABB1. ∴BC⊥A1D. ∵BC∩BB1=B. ∴A1D⊥平面BCC1B1. 故∠A1CD为直线A1C与平面BCC1B1所成的角. 在矩形BCC1B1中.DC=. ∵四边形A1ABB1是菱形.∠A1AB=60°, AB=4.∴A1D=2. ∴tan∠A1CD===. (3)解 ∵B1C1∥BC.∴B1C1∥平面A1BC. ∴C1到平面A1BC的距离即为B1到平面A1BC的距离. 连接AB1.AB1与A1B交于点O. ∵四边形A1ABB1是菱形.∴B1O⊥A1B. ∵平面CA1B⊥平面A1BB1.∴B1O⊥平面A1BC. ∴B1O即为C1到平面A1BC的距离. ∵B1O=2.∴C1到平面A1BC的距离为2.
网址：http://m.1010jiajiao.com/timu_id_4039545[举报]
如图所示，在三棱柱ABC—A1B1C1中，四边形A1ABB1是菱形，四边形BCC1B1是矩形，AB⊥BC，CB=3，AB=4，∠A1AB=60°.
（1）求证：平面CA1B⊥平面A1ABB1；
（2）求直线A1C与平面BCC1B1所成角的正切值；
（3）求点C1到平面A1CB的距离.
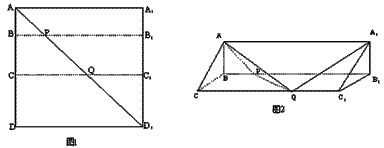
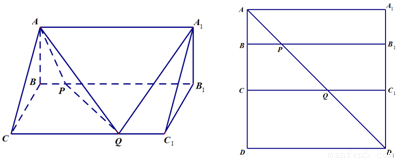
如图所示，在边长为12的正方形ADD1A1中，点B，C在线段AD上，且AB=3，BC=4，作BB1∥AA1，分别交A1D1、AD1于点B1、P，作CC1∥AA1，分别交A1D1、AD1于点C1、Q，将该正方形沿BB1、CC1折叠，使得DD1与AA1重合，构成如图所示的三棱柱ABC-A1B1C1．（1）求证：AB⊥平面BCC1B1；
（2）求四棱锥A-BCQP的体积；
（3）求二面角A-PQ-C的大小．
如图所示，在边长为12的正方形ADD1A1中，点B，C在线段AD上，且AB=3，BC=4，作BB1∥AA1，分别交A1D1、AD1于点B1、P，作CC1∥AA1，分别交A1D1、AD1于点C1、Q，将该正方形沿BB1、CC1折叠，使得DD1与AA1重合，构成如图所示的三棱柱ABC-A1B1C1．
