摘要:如图...-. 是曲线:上的个点.点()在轴的正半轴上.且是正三角形(是坐标原点). (Ⅰ)写出.., (Ⅱ)求出点()的 横坐标关于的表达式并证明. 1解:以有点为原点.极轴为轴正半轴.建立平面直角坐标系.两坐标系中取相同的长度单位.(1)由得. 所以. 即为圆的直角坐标方程.------.3分 同理为圆的直角坐标方程.------.6分 (2)由 解得. 即圆.圆交于点和.过交点的直线的直角坐标方程为.------.10分 2解:分别记甲.乙.丙经第一次烧制后合格为事件 (1)设表示第一次烧制后恰好有一件合格.则 .------.5分 (2)解法一:因为每件工艺品经过两次烧制后合格的概率均为. 所以 故.------.10分 解法二:分别记甲.乙.丙经过两次烧制后合格为事件. 则 所以 于是------.10分
网址:http://m.1010jiajiao.com/timu_id_4038183[举报]
 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(1)、选修4-1:几何证明选讲
如图,∠PAQ是直角,圆O与AP相切于点T,与AQ相交于两点B,C.求证:BT平分∠OBA
(2)选修4-2:矩阵与变换(本小题满分10分)
若点A(2,2)在矩阵M=
|
(3)选修4-2:矩阵与变换(本小题满分10分)
在极坐标系中,A为曲线ρ2+2ρcosθ-3=0上的动点,B为直线ρcosθ+ρsinθ-7=0上的动点,求AB的最小值.
(4)选修4-5:不等式选讲(本小题满分10分)
已知a1,a2…an都是正数,且a1•a2…an=1,求证:(2+a1)(2+a2)…(2+an)≥3n.
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(1)、选修4-1:几何证明选讲
如图,∠PAQ是直角,圆O与AP相切于点T,与AQ相交于两点B,C.求证:BT平分∠OBA
(2)选修4-2:矩阵与变换(本小题满分10分)
若点A(2,2)在矩阵 对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵
对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵
(3)选修4-2:矩阵与变换(本小题满分10分)
在极坐标系中,A为曲线ρ2+2ρcosθ-3=0上的动点,B为直线ρcosθ+ρsinθ-7=0上的动点,求AB的最小值.
(4)选修4-5:不等式选讲(本小题满分10分)
已知a1,a2…an都是正数,且a1•a2…an=1,求证:(2+a1)(2+a2)…(2+an)≥3n.
 查看习题详情和答案>>
查看习题详情和答案>>
若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(1)、选修4-1:几何证明选讲
如图,∠PAQ是直角,圆O与AP相切于点T,与AQ相交于两点B,C.求证:BT平分∠OBA
(2)选修4-2:矩阵与变换(本小题满分10分)
若点A(2,2)在矩阵
 对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵
对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵(3)选修4-2:矩阵与变换(本小题满分10分)
在极坐标系中,A为曲线ρ2+2ρcosθ-3=0上的动点,B为直线ρcosθ+ρsinθ-7=0上的动点,求AB的最小值.
(4)选修4-5:不等式选讲(本小题满分10分)
已知a1,a2…an都是正数,且a1•a2…an=1,求证:(2+a1)(2+a2)…(2+an)≥3n.
 查看习题详情和答案>>
查看习题详情和答案>>
【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
A.选修4-1:几何证明选讲
如图,已知AB,CD是圆O的两条弦,且AB是线段CD的 垂直平分线,若AB=6,CD=2 ,求线段AC的长度.
,求线段AC的长度.
B.选修4-2:矩阵与变换(本小题满分10分)
已知矩阵M= 的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.
的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.
C.选修4-4:坐标系与参数方程(本小题满分10分)
在平面直角坐标系xOy中,已知曲线C的参数方程是 (α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
(α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
D.选修4-5:不等式选讲(本小题满分10分)
已知关于x的不等式|ax-1|+|ax-a|≥1的解集为R,求正实数a的取值范围.
 查看习题详情和答案>>
查看习题详情和答案>>
A.选修4-1:几何证明选讲
如图,已知AB,CD是圆O的两条弦,且AB是线段CD的 垂直平分线,若AB=6,CD=2
 ,求线段AC的长度.
,求线段AC的长度.B.选修4-2:矩阵与变换(本小题满分10分)
已知矩阵M=
 的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.
的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.C.选修4-4:坐标系与参数方程(本小题满分10分)
在平面直角坐标系xOy中,已知曲线C的参数方程是
 (α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
(α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.D.选修4-5:不等式选讲(本小题满分10分)
已知关于x的不等式|ax-1|+|ax-a|≥1的解集为R,求正实数a的取值范围.
 查看习题详情和答案>>
查看习题详情和答案>>
【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
A.选修4-1:几何证明选讲
如图,已知AB,CD是圆O的两条弦,且AB是线段CD的 垂直平分线,若AB=6,CD=2 ,求线段AC的长度.
,求线段AC的长度.
B.选修4-2:矩阵与变换(本小题满分10分)
已知矩阵M= 的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.
的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.
C.选修4-4:坐标系与参数方程(本小题满分10分)
在平面直角坐标系xOy中,已知曲线C的参数方程是 (α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
(α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
D.选修4-5:不等式选讲(本小题满分10分)
已知关于x的不等式|ax-1|+|ax-a|≥1的解集为R,求正实数a的取值范围.
 查看习题详情和答案>>
查看习题详情和答案>>
A.选修4-1:几何证明选讲
如图,已知AB,CD是圆O的两条弦,且AB是线段CD的 垂直平分线,若AB=6,CD=2
 ,求线段AC的长度.
,求线段AC的长度.B.选修4-2:矩阵与变换(本小题满分10分)
已知矩阵M=
 的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.
的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.C.选修4-4:坐标系与参数方程(本小题满分10分)
在平面直角坐标系xOy中,已知曲线C的参数方程是
 (α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
(α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.D.选修4-5:不等式选讲(本小题满分10分)
已知关于x的不等式|ax-1|+|ax-a|≥1的解集为R,求正实数a的取值范围.
 查看习题详情和答案>>
查看习题详情和答案>>
【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
A.选修4-1:几何证明选讲
如图,已知AB,CD是圆O的两条弦,且AB是线段CD的 垂直平分线,若AB=6,CD=2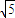 ,求线段AC的长度.
,求线段AC的长度.
B.选修4-2:矩阵与变换(本小题满分10分)
已知矩阵M= 的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.
的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.
C.选修4-4:坐标系与参数方程(本小题满分10分)
在平面直角坐标系xOy中,已知曲线C的参数方程是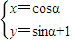 (α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
(α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
D.选修4-5:不等式选讲(本小题满分10分)
已知关于x的不等式|ax-1|+|ax-a|≥1的解集为R,求正实数a的取值范围.
 查看习题详情和答案>>
查看习题详情和答案>>
A.选修4-1:几何证明选讲
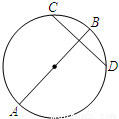
如图,已知AB,CD是圆O的两条弦,且AB是线段CD的 垂直平分线,若AB=6,CD=2
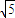 ,求线段AC的长度.
,求线段AC的长度.B.选修4-2:矩阵与变换(本小题满分10分)
已知矩阵M=
 的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.
的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.C.选修4-4:坐标系与参数方程(本小题满分10分)
在平面直角坐标系xOy中,已知曲线C的参数方程是
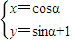 (α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
(α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.D.选修4-5:不等式选讲(本小题满分10分)
已知关于x的不等式|ax-1|+|ax-a|≥1的解集为R,求正实数a的取值范围.
 查看习题详情和答案>>
查看习题详情和答案>>