摘要: 如图.四边形ABCD为矩形.BC上平面ABE.F为CE上的点.且BF⊥平面ACE. (1)求证:AE⊥BE, (2)设点M为线段AB的中点.点N为线段CE的中点. 求证:MN∥平面DAE.
网址:http://m.1010jiajiao.com/timu_id_4038143[举报]
(本小题满分14分)如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PA的长为2,且PA与AB、AD的夹角都等于600,![]() 是PC的中点,设
是PC的中点,设![]() .
.
(1)试用![]() 表示出向量
表示出向量![]() ;
;
(2)求![]() 的长.
的长.

(本小题满分14分)如图,已知四面体ABCD的四个面均为锐角三角形,E、F、G、H分别为边AB、BC、CD、DA上的点,BD∥平面EFGH,且EH=FG.

(1) 求证:HG∥平面ABC;
(2) 请在面ABD内过点E作一条线段垂直于AC,并给出证明.
查看习题详情和答案>>
(本小题满分14分)如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PA的长为2,且PA与AB、AD的夹角都等于600, 是PC的中点,设
是PC的中点,设 .
.
(1)试用 表示出向量
表示出向量 ;
;
(2)求 的长.
的长.

查看习题详情和答案>>

 是PC的中点,设
是PC的中点,设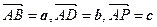 .
.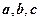 表示出向量
表示出向量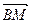 ;
;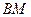 的长.
的长.