摘要:20. 已知数列中..且对时.有. (Ⅰ)设数列满足.证明数列为等比数列.并求数列的通项公式, (Ⅱ)记.求数列的前n项和Sn. (Ⅰ) 证明:由条件.得. 则.--------------2分 即.所以.. 所以是首项为2.公比为2的等比数列. -------------4分 .所以. 两边同除以.可得.-------------------6分 于是为以首项.-为公差的等差数列. 所以.------------------8分 (Ⅱ).令.则. 而. ∴. -----------------------12分 . ∴.------14分 令Tn=. ① 则2Tn=. ② ①-②.得Tn=.Tn=. ∴.-----------------------16分 评讲建议: 此题主要考查数列的概念.等差数列.等比数列.数列的递推公式.数列的通项求法.数列前n项和的求法.作新数列法.错项相消法.裂项法等知识与方法.同时考查学生的分析问题与解决问题的能力.逻辑推理能力及运算能力.讲评时着重在正确审题.怎样将复杂的问题化成简单的问题.本题主要将一个综合的问题分解成几个常见的简单问题.事实上本题包含了好几个常见的数列题.本题还有一些另外的解法.如第一问的证明还可以直接代. B.附加题部分
网址:http://m.1010jiajiao.com/timu_id_4038096[举报]
(本小题满分16分)
已知数列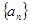 中,
中,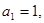 且点
且点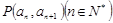 在直线
在直线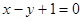 上.
上.
(1)求数列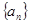 的通项公式;
的通项公式;
 (2)若函数
(2)若函数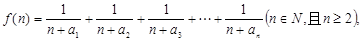 求函数
求函数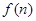 的最小值;
的最小值;
(3)设 表示数列
表示数列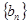 的前
的前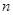 项和.试问:是否存在关于
项和.试问:是否存在关于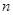 的整式
的整式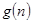 ,使得
,使得
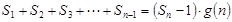 对于一切不小于2的自然数
对于一切不小于2的自然数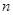 恒成立? 若存在,写出
恒成立? 若存在,写出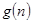 的解析式,并加以证明;若不存在,试说明理由.
的解析式,并加以证明;若不存在,试说明理由.
查看习题详情和答案>>
(本小题满分16分)
已知数列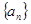 中,
中,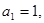 且点
且点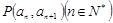 在直线
在直线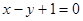 上.
上.
(1)求数列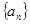 的通项公式;
的通项公式;
 (2)若函数
(2)若函数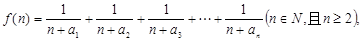 求函数
求函数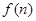 的最小值;
的最小值;
(3)设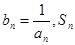 表示数列
表示数列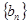 的前
的前 项和.试问:是否存在关于
项和.试问:是否存在关于 的整式
的整式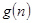 ,使得
,使得
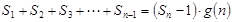 对于一切不小于2的自然数
对于一切不小于2的自然数 恒成立? 若存在,写出
恒成立? 若存在,写出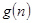 的解析式,并加以证明;若不存在,试说明理由.
的解析式,并加以证明;若不存在,试说明理由.
已知数列
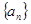 中,
中,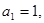 且点
且点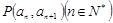 在直线
在直线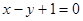 上.
上.(1)求数列
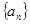 的通项公式;
的通项公式; (2)若函数
(2)若函数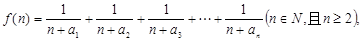 求函数
求函数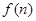 的最小值;
的最小值;(3)设
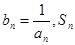 表示数列
表示数列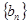 的前
的前 项和.试问:是否存在关于
项和.试问:是否存在关于 的整式
的整式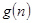 ,使得
,使得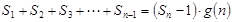 对于一切不小于2的自然数
对于一切不小于2的自然数 恒成立? 若存在,写出
恒成立? 若存在,写出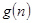 的解析式,并加以证明;若不存在,试说明理由.
的解析式,并加以证明;若不存在,试说明理由. (本小题满分16分)已知数列![]() 是以
是以![]() 为公差的等差数列,数列
为公差的等差数列,数列![]() 是以
是以![]() 为公比的等比数列.
为公比的等比数列.
(Ⅰ)若数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() ,求整数
,求整数![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,试问数列![]() 中是否存在一项
中是否存在一项![]() ,使得
,使得![]() 恰好可以表示为该数列中连续
恰好可以表示为该数列中连续![]() 项的和?请说明理由;
项的和?请说明理由;
(Ⅲ)若![]() (其中
(其中![]() ,且(
,且(![]() )是(
)是(![]() )的约数),
)的约数),
求证:数列![]() 中每一项都是数列
中每一项都是数列![]() 中的项.
中的项.
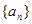 ,
,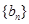 ,且满足
,且满足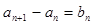 (
(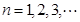 ).
).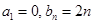 ,求数列
,求数列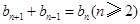 ,且
,且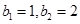 .记
.记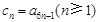 ,求证:数列
,求证:数列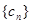 为常数列;
为常数列; ,且
,且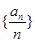 中必有某数重复出现无数次,求首项
中必有某数重复出现无数次,求首项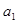 应满足的条件.
应满足的条件.