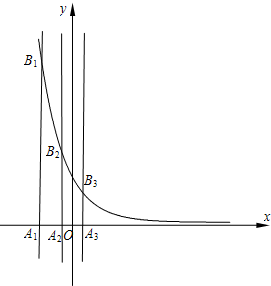（2006•蚌埠二模）已知等差数列{a_n}的首项为p，公差为d（d＞0）．对于不同的自然数n，直线x=a_n与x轴和指数函数f(x)=(

1

2

)x的图象分别交于点A_n与B_n（如图所示），记B_n的坐标为（a_n，b_n），直角梯形A₁A₂B₂B₁、A₂A₃B₃B₂的面积分别为s₁和s₂，一般地记直角梯形A_nA_n+1B_n+1B_n的面积为s_n．
（1）求证数列{s_n}是公比绝对值小于1的等比数列；
（2）设{a_n}的公差d=1，是否存在这样的正整数n，构成以b_n，b_n+1，b_n+2为边长的三角形？并请说明理由；
（3）（理科做，文科不做）设{a_n}的公差d=1，是否存在这样的实数p使得（1）中无穷等比数列{s_n}各项的和S＞2010？如果存在，给出一个符合条件的p值；如果不存在，请说明理由．（参考数据：2¹⁰=1024）