摘要:例1. 如图.已知四棱锥的底面是直角梯形...侧面底面. (1)与是否相互垂直.请证明你的结论, (2)求二面角的大小, (3)求证:平面⊥平面. 解:(1)与相互垂直.证明如下: 取的中点.连结.交于点,连结. ∵.∴.又∵平面⊥平面. 平面∩平面.∴⊥平面. 在梯形中.可得. ∴. 即. ∴ . (2)连结. 由⊥平面..可得. ∴为二面角的平面角. 设.则在中. ∴二面角为 . (3)取的中点.连结.由题意知:平面⊥平面. 则同“(1) 可得平面. 取的中点.连结.则由. .得四边形为平行四边形. ∴. ∴⊥平面.∴平面⊥平面. 解答二: 取的中点.由侧面⊥底面. 是等边三角形. 得⊥底面. 以为原点.以所在直线为轴. 过点与平行的直线为轴. 建立如图所示的空间直角坐标系. 设.则在直角梯形中.. 在等边三角形中..∴ (1)与相互垂直.证明如下:∵ ∴. (2)连结.设与相交于点,连结. 由得. 又∵为在平面内的射影. ∴.为二面角的平面角. 在中.. 在中.. ∴二面角为. (3)取的中点.连结.则的坐标为. 又.. ∴ . ∴ ∴⊥平面. ∴平面⊥平面. 小结:三垂线定理是求二面角的平面角的又一常用方法. 例2.在的二面角中..已知.到的距离分别是和.且..在的射影分别为..求:(1)的长度,(2)和棱所成的角. 例3.棱长为4的正方体中.是正方形的中心.点在棱上.且. (Ⅰ)求直线与平面所成的角的大小(结果用反三角函数值表示), (Ⅱ)设点在平面上的射影是.求证:. 例4. 在三棱锥中.是边长为的正三角形.平面平面..分别是的中点. (1)证明, (2)求二面角的大小, (3)求点到平面的距离. 例5. 如图.直四棱柱ABCD-A1B1C1D1的侧棱AA1的长为a.底面ABCD是边长AB=2a.BC=a的矩形.又E是C1D1的中点, (1)CE与BD1所成角的余弦值, (2)求证:平面BCE⊥平面BDE, (3)求二面角B-DC1-C的平面角的大小
网址:http://m.1010jiajiao.com/timu_id_4037498[举报]
 的底面
的底面 是直角梯形,
是直角梯形, ,
, ,侧面
,侧面 为正三角形,
为正三角形, ,
, .如图所示.
.如图所示.
 平面
平面 .
.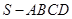 的底面
的底面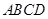 是直角梯形,
是直角梯形,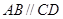 ,
,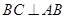 ,侧面
,侧面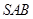 为正三角形,
为正三角形,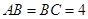 ,
,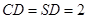 .如图所示.
.如图所示.
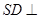 平面
平面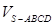 .
.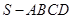 的底面
的底面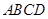 是直角梯形,
是直角梯形,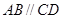 ,
,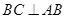 ,侧面
,侧面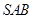 为正三角形,
为正三角形,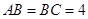 ,
,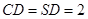 .如图所示.
.如图所示.
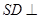 平面
平面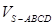 .
.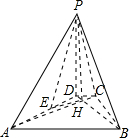 如图,已知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高,E为AD中点
如图,已知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高,E为AD中点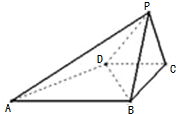 如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD.
如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD.