摘要：23． 解:(1)由题意.当MN和AB之间的距离为0.5米时.MN应位于DC下方.且此时△EMN中MN边上的高为0.5米. 所以.S△EMN= =0.5. 即△EMN的面积为0.5平方米. ----2分 (2)①如图1所示.当MN在矩形区域滑动. 即0＜x≤1时. △EMN的面积S= = ,--3分 ②如图2所示.当MN在三角形区域滑动. 即1＜x＜ 时. 如图.连接EG.交CD于点F.交MN于点H. ∵ E为AB中点. ∴ F为CD中点.GF⊥CD,且FG＝ . 又∵ MN∥CD. ∴ △MNG∽△DCG． ∴ .即 ．--4分 故△EMN的面积S＝ ＝ , -------5分 综合可得: -----------6分 (3)①当MN在矩形区域滑动时. .所以有 ,---7分 ②当MN在三角形区域滑动时.S= . 因而.当 (米)时,S得到最大值. 最大值S= = = . -----9分 ∵ . ∴ S有最大值.最大值为 平方米. -----------10分
网址：http://m.1010jiajiao.com/timu_id_4035845[举报]
（本题满分10分）如图，小明家在A处，门前有一口池塘，隔着池塘有一条公路l，AB是A到l的小路.
现新修一条路AC到公路l. 小明测量出∠ACD=30º，∠ABD=45º，BC=50m. 请你帮小明计算他家到公路l的距离AD的长度（精确到0.1m；参考数据：
，
）.
查看习题详情和答案>>
（本题满分10分）如图，BD是直径，过⊙O上一点A作⊙O切线交DB延长线于P，过B点作BC∥PA交⊙O于C，连接AB、AC ，
1.（1）求证：AB = AC
2.（2）若PA= 10 ，PB = 5 ，求⊙O半径．
查看习题详情和答案>>
（本题满分10分）如图，已知二次函数
的图象的顶点为
．二次函数
的图象与
轴交于原点
及另一点
，它的顶点
在函数的图象的对称轴上．
（1）求点与点的坐标；
（2）当四边形
为菱形时，求函数的关系式．
查看习题详情和答案>>
（本题满分10分）
如图，已知OA⊥OB，OA＝8，OB＝6，以AB为边作矩形ABCD，使AD＝a，过点D作DE垂直OA的延长线交于点E．
（1）求证：△OAB∽△EDA；
（2）当a为何值时，△OAB与△EDA全等？并求出此时点C到OE的距离．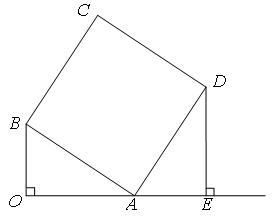
查看习题详情和答案>>
如图，已知OA⊥OB，OA＝8，OB＝6，以AB为边作矩形ABCD，使AD＝a，过点D作DE垂直OA的延长线交于点E．
（1）求证：△OAB∽△EDA；
（2）当a为何值时，△OAB与△EDA全等？并求出此时点C到OE的距离．
查看习题详情和答案>>
（11·贵港）（本题满分10分）
随着人们经济收入的不断提高及汽车产业的快速发展，汽车已越来越多地进入普通家庭．据某市交通部门统计，2008年底该市汽车拥有量为75万辆，而截止到2010年底，该市的汽车拥有量已达108万辆．
（1）求2008年底至2010年底该市汽车拥有量的年平均增长率；
（2）为了保护城市环境，缓解汽车拥堵状况，该市交通部门拟控制汽车总量，要求到2012
年底全市汽车拥有量不超过125.48万辆；另据统计，从2011年初起，该市此后每年报废的
汽车数量是上年底汽车拥有量的10%假设每年新增汽车数量相同，请你估算出该市从2011
年初起每年新增汽车数量最多不超过多少万辆． 查看习题详情和答案>>
随着人们经济收入的不断提高及汽车产业的快速发展，汽车已越来越多地进入普通家庭．据某市交通部门统计，2008年底该市汽车拥有量为75万辆，而截止到2010年底，该市的汽车拥有量已达108万辆．
（1）求2008年底至2010年底该市汽车拥有量的年平均增长率；
（2）为了保护城市环境，缓解汽车拥堵状况，该市交通部门拟控制汽车总量，要求到2012
年底全市汽车拥有量不超过125.48万辆；另据统计，从2011年初起，该市此后每年报废的
汽车数量是上年底汽车拥有量的10%假设每年新增汽车数量相同，请你估算出该市从2011
年初起每年新增汽车数量最多不超过多少万辆． 查看习题详情和答案>>