网址：http://m.1010jiajiao.com/timu_id_4034744[举报]
为了研究平抛物体的运动，可做下面的实验：如图甲所示，用小锤打击弹性金属片，B球就水平飞出，同时A球被松开，做自由落体运动，两球同时落到地面；如图乙所示的实验：将两个完全相同的斜滑道固定在同一竖直面内，最下端水平．把两个质量相等的小钢球从斜面的同一高度由静止同时释放，滑道2与光滑水平板吻接，则将观察到的现象是球1落到水平木板上击中球2，这两个实验说明（ ）一般的曲线运动可以分成很多小段，每小段都可以看成圆周运动的一部分，即把整条曲线用一系列不同半径的小圆弧来代替．如图4－3－12甲所示，曲线上的A点的曲率圆定义为：通过A点和曲线上紧邻A点两侧的两点作一圆，在极限情况下，这个圆就叫做A点的曲率圆，其半径ρ叫做A点的曲率半径．现将一物体沿与水平面成α角的方向以速度v0抛出，如图4－3－12乙所示．则在其轨迹最高点P处的曲率半径是 ( )．
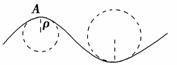
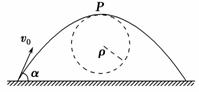
甲 乙
图4－3－12
A.
B.
C.
D.
竖直方向的抛体运动、斜抛运动
1．竖直下抛运动：
(1)定义：将物体以一定的初速度________竖直抛出，物体只在重力作用下运动．
(2)规律：①速度公式：________ ②位移公式：________
2．竖直上抛运动：
(1)定义：将物体以一定的初速度________竖直抛出，物体只在重力作用下运动．
(2)竖直上抛运动的特点：是一种________直线运动，上升过程与下降过程，运动具有________．
(3)常用研究方法——分段法：竖直上抛运动可分为上升和下降两个阶段，上升阶段是________直线运动，下降阶段是________直线运动
(4)规律：①速度公式：________ ②位移公式：________ ③上升至最高点的时间：________ ④上升能达到的最大高度________．
3．斜抛运动的特点：可看成是竖直方向的________运动和水平方向的________运动．
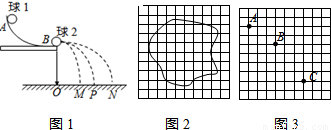
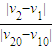，其中v10和v20分别是碰撞前两物体的速度，v1和v2分别是碰撞后两物体的速度．某同学用验证动量守恒定律的实验装置（如图1所示）求弹性碰撞的恢复系数，实验中使用半径相等的钢质小球1和2，（它们之间的碰撞可近似为弹性碰撞），且小球1的质量大于小球2的质量，小球2碰撞前静止．在实验中需要用刻度尺测量的物理量有______、______和______的长度，写出用测量量表示的恢复系数的表达式：______．（Ⅱ）在用油膜法估测油酸分子直径大小的实验中，将1滴配置好的油酸酒精溶液滴入盛水的浅盘中，让油膜在水面上尽可能散开，待液面稳定后，在水面上形成油酸的______油膜；把带有方格的玻璃板放在浅盘上，在玻璃板上描绘出油膜的边界轮廓，形状如图2所示．已知坐标方格边长为1cm，则油膜的面积为______cm2．
（Ⅲ）如图3为一个小球做平抛运动的闪光照片的一部分，图中竖直背景方格的实际边长均为5cm，那么照片的闪光频率为______Hz；小球做平抛运动的初速度大小为______m/s．（g=10m/s2）
查看习题详情和答案>>
法国数学家兼天文学家拉普拉斯于1796年曾预言：“一个密度如地球而直径约为太阳250倍的发光恒星，由于其引力作用，将不允许任何物体（包括光）离开它．由于这个原因，宇宙中有些天体将不会被我们看见．”这种奇怪的天体也就是爱因斯坦在广义相对论中预言的“黑洞（black hole）”．
已知对任何密度均匀的球形天体，v2恒为v1的
| 2 |
（1）求质量为M、半径为R的星体逃离速度v2的大小；
（2）如果有一黑洞，其质量为地球的10倍，则其半径应为多少？
（3）若宇宙中一颗发光恒星，直径为太阳的248倍，密度和地球相同，试通过计算分析，该恒星能否被我们看见．