摘要：例1 如图6是定义在闭区间[-5.5]上的函数的图象.根据图象说出的单调区间.以及在每一单调区间上.函数是增函数还是减函数. 解:函数的单调区间有[-5.-2).[-2.1).[1.3).[3.5].其中在区间[-5.-2).[1.3)上是减函数.在区间[-2.1).[3.5]上是增函数. 说明:函数的单调性是对某个区间而言的.对于单独的一点.由于它的函数值是唯一确定的常数.因而没有增减变化.所以不存在单调性问题,另外.中学阶段研究的主要是连续函数或分段连续函数.对于闭区间上的连续函数来说.只要在开区间上单调.它在闭区间上也就单调.因此.在考虑它的单调区间时.包括不包括端点都可以,还要注意.对于在某些点上不连续的函数.单调区间不包括不连续点. 例2 证明函数在R上是增函数. 证明:设是R上的任意两个实数.且<.则 -=(3+2)-(3+2)=3(-), 由<x,得-<0 ,于是-<0,即 <. ∴在R上是增函数. 例3 证明函数在(0,+)上是减函数. 证明:设,是(0,+)上的任意两个实数.且<. 则-=-=, 由,∈(0,+ ).得>0, 又由<,得->0 ,于是->0,即> ∴在(0,+ )上是减函数. 例4．讨论函数在内的单调性. 解:∵.对称轴 ∴若,则在内是增函数, 若则在内是减函数,在[a,2]内是增函数 若,则在内是减函数.
网址：http://m.1010jiajiao.com/timu_id_4034379[举报]
读图分析解答：设定义在闭区间[-4，4]上的函数y=f（x）的图象如图所示（图中坐标点都是实心点），完成以下几个问题：（1）x∈[-2，3]时，y的取值范围是
（2）该函数的值域为
（3）若y=f（x）的定义域为[-4，4]，则函数y=f（x+1）的定义域为
（4）写出该函数的一个单调增区间为
（5）使f（x）=3（x∈[-4，4]）的x的值有
（6）函数y=f（x）是区间x∈[-4，4]的
（7）若方程f（x）=5-3a在区间[-4，4]上有且只有三个解，求f（a）的取值范围． 查看习题详情和答案>>
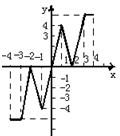读图分析解答：设定义在闭区间[-4，4]上的函数y=f（x）的图象如图所示（图中坐标点都是实心点），完成以下几个问题：