网址:http://m.1010jiajiao.com/timu_id_4034378[举报]
设f(x)是定义在[0,1]上的函数,若存在x*∈(0,1),使得f(x)在[0,x*]上单调递增,在[x*,1]上单调递减,则称f(x)为[0,1]上的单峰函数,x*为峰点,包含峰点的区间为含峰区间.对任意的[0,1]上的单峰函数f(x),下面研究缩短其含峰区间长度的方法.
(I)证明:对任意的 ∈(O,1),
∈(O,1), ,若f(
,若f( )≥f(
)≥f(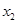 ),则(0,
),则(0,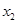 )为含峰区间:若f(
)为含峰区间:若f( )
) f(
f(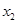 ),则
),则 为含峰区间:
为含峰区间:
(II)对给定的r(0<r<0.5),证明:存在 ∈(0,1),满足
∈(0,1),满足 ,使得由(I)所确定的含峰区间的长度不大于0.5+r:
,使得由(I)所确定的含峰区间的长度不大于0.5+r:
(III)选取 ∈(O,1),,由(I)可确定含峰区间为
∈(O,1),,由(I)可确定含峰区间为 或
或 ,在所得的含峰区间内选取
,在所得的含峰区间内选取 ,由
,由 与
与 或
或 与
与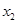 类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0,
类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0,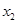 )的情况下,试确定的值
)的情况下,试确定的值 ,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0. 34(区间长度等于区间的右端点与左端点之差)
,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0. 34(区间长度等于区间的右端点与左端点之差)
查看习题详情和答案>>
(I)证明:对任意的
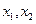 ∈(O,1),
∈(O,1),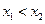 ,若f(
,若f(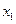 )≥f(
)≥f(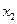 ),则(0,
),则(0,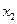 )为含峰区间:若f(
)为含峰区间:若f(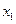 )
)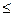 f(
f(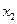 ),则
),则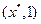 为含峰区间:
为含峰区间:(II)对给定的r(0<r<0.5),证明:存在
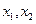 ∈(0,1),满足
∈(0,1),满足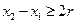 ,使得由(I)所确定的含峰区间的长度不大于0.5+r:
,使得由(I)所确定的含峰区间的长度不大于0.5+r:(III)选取
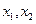 ∈(O,1),,由(I)可确定含峰区间为
∈(O,1),,由(I)可确定含峰区间为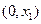 或
或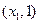 ,在所得的含峰区间内选取
,在所得的含峰区间内选取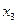 ,由
,由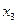 与
与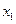 或
或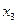 与
与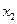 类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0,
类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0,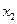 )的情况下,试确定的值
)的情况下,试确定的值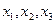 ,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0. 34(区间长度等于区间的右端点与左端点之差)
,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0. 34(区间长度等于区间的右端点与左端点之差)①奇函数的图象一定过原点;
②函数y=
| ||
| |x+2|-2 |
③奇函数f(x)在[a,b]上为增函数,则函数f(x)在[-b,-a]上为减函数;
④定义在R上的函数y=f(x),则函数y=f(x-1)与y=f(1-x)的图象关于直线x=1对称;
其中正确命题的序号是
对任意的[0,1]上的单峰函数f(x),下面研究缩短其含峰区间长度的方法.
(I)证明:对任意的x1,x2∈(0,1),x1<x2,若f(x1)≥f(x2),则(0,x2)为含峰区间;若f(x1)≤f(x2),则(x1,1)为含峰区间;
(II)对给定的r(0<r<0.5),证明:存在x1,x2∈(0,1),满足x2-x1≥2r,使得由(I)所确定的含峰区间的长度不大于 0.5+r;
(III)选取x1,x2∈(0, 1),x1<x2,由(I)可确定含峰区间为(0,x2)或(x1,1),在所得的含峰区间内选取x3,由x3与x1或x3与x2类似地可确定一个新的含峰区间.在第一次确定的含峰区间为(0,x2)的情况下,试确定x1,x2,x3的值,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0.34.
(区间长度等于区间的右端点与左端点之差)
查看习题详情和答案>>设f(x)是定义在[0,1]上的函数,若存在x*∈(0,1),使得f(x)在[0,x*]上单调递增,在[x*,1]上单调递减,则称f(x)为[0,1]上的单峰函数,x*为峰点,包含峰点的区间为含峰区间.对任意的[0,1]上的单峰函数f(x),下面研究缩短其含峰区间长度的方法:
(1)证明:对任意的x1,x2∈(0,1),x1<x2,若f(x1)≥f(x2),则(0,x2)为含峰区间;若f(x1)≤f(x2),则(x1,1)为含峰区间;
(2)对给定的r(0<r<0.5),证明存在x1,x2∈(0,1),满足x2-x1≥2r,使得由(1)所确定的含峰区间的长度不大于0.5+r;
(3)选取x1,x2∈(0,1),x1<x2,由(1)可确定含峰区间为(0,x2)或(x1,1),在所得的含峰区间内选取x3,由x3与x1或x3与x2类似地可确定一个新的含峰区间.在第一次确定的含峰区间为(0,x2)的情况下,试确定x1,x2,x3的值,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0.34.
(区间长度等于区间的右端点与左端点之差)