摘要：1．要在本章的教学中.应该根据教学实际.启发学生不断提出问题.研究问题.在对于正弦定理和余弦定理的证明的探究过程中.应该因势利导.根据具体教学过程中学生思考问题的方向来启发学生得到自己对于定理的证明.如对于正弦定理.可以启发得到有应用向量方法的证明.对于余弦定理则可以启发得到三角方法和解析的方法.在应用两个定理解决有关的解三角形和测量问题的过程中.一个问题也常常有多种不同的解决方案.应该鼓励学生提出自己的解决办法.并对于不同的方法进行必要的分析和比较.对于一些常见的测量问题甚至可以鼓励学生设计应用的程序.得到在实际中可以直接应用的算法.
网址：http://m.1010jiajiao.com/timu_id_4033479[举报]
某地有三家工厂，分别位于矩形ABCD 的顶点A,B 及CD的中点P 处，已知AB=20km,CB =10km ，为了处理三家工厂的污水，现要在矩形ABCD
的区域中（含边界），且与A,B等距离的一点O 处建造一个污水处理厂，并铺设排污管道AO,BO,OP ，设排污管道的总长为
km．
（Ⅰ）设∠BAO=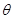
(rad)，将表示成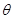的函数关系式；
（Ⅱ）请用（Ⅰ）中的函数关系式，确定污水处理厂的位置，使三条排污管道总长度最短．
查看习题详情和答案>>
某社区的常住人口中，有成年人3200人，其中有无业人员1000人，从事个体劳动的有1160人，有固定收入的上班人员1040人，如果想通过调查其中160人的生活消费情况来了解本社区群众的生活消费情况，考虑到由于各种人员情况的差异，而同一阶层人员的差异较小，问应当采取怎样的抽取方法？从事个体劳动的人员中应抽查多少人？在本问题的设计中还有哪些重要因素将影响调查效果？应怎样改进抽查方案使效果更加客观？
查看习题详情和答案>>