摘要: 正整数集合的最小元素为.最大元素为.并且各元素可以从小到大排成一个公差为的等差数列.则并集中元素有 个. 例题选讲 例1 已知等比数列的各项均为正数.且公比不等于1.数列对任意正整数n.均有: 成立.又. (Ⅰ)求数列的通项公式及前n项和, (Ⅱ)在数列中依次取出第1项.第2项.第4项.第8项.--.第项.--.组成一个新数列.求数列的前n项和, (Ⅲ)当时.比较与的大小. 例2如图.是曲线 上的个点.点在轴的正半轴上.是正三角形(是坐标原点) . (Ⅰ) 写出, (Ⅱ)求出点的横坐标关于的表达式, (Ⅲ)设.若对任意正整数.当时.不等式恒成立.求实数的取值范围. 例3已知函数.函数其中一个零点为5.数列满足.且. (1)求数列通项公式,(2)试证明,(3)设.试探究数列是否存在最大项和最小项?若存在求出最大项和最小项.若不存在.说明理由. 课后练习
网址:http://m.1010jiajiao.com/timu_id_4031354[举报]
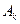 的最小元素为
的最小元素为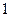 ,最大元素为
,最大元素为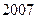 ,并且各元素可以从小到大排成一个公差为
,并且各元素可以从小到大排成一个公差为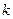 的等差数列,则并集
的等差数列,则并集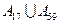 中的元素个数为( ).
中的元素个数为( ).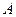 、
、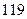
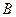 、
、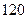 ;
; 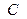 、
、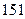 ;
; 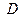 、
、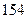 .
.