摘要：本讲内容主要有空间直角坐标系.空间向量的坐标表示.空间向量的坐标运算.平行向量.垂直向量坐标之间的关系以及中点公式.空间直角坐标系是选取空间任意一点O和一个单位正交基底{i.j.k}建立坐标系.对于O点的选取要既有作图的直观性.而且使各点的坐标.直线的坐标表示简化.要充分利用空间图形中已有的直线的关系和性质,空间向量的坐标运算同平面向量类似.具有类似的运算法则.一个向量在不同空间的表达方式不一样.实质没有改变.因而运算的方法和运算规律结论没变.如向量的数量积a·b=|a|·|b|cos<a.b>在二维.三维都是这样定义的.不同点仅是向量在不同空间具有不同表达形式.空间两向量平行时同平面两向量平行时表达式不一样.但实质是一致的.即对应坐标成比例.且比值为.对于中点公式要熟记. 对本讲内容的考查主要分以下三类:1．以选择.填空题型考查本章的基本概念和性质 此类题一般难度不大.用以解决有关长度.夹角.垂直.判断多边形形状等问题.
网址：http://m.1010jiajiao.com/timu_id_4030667[举报]
（辽宁卷理19）如图，在棱长为1的正方体
中，AP=BQ=b（0<b<1），截面PQEF∥
，截面PQGH∥
．
（Ⅰ）证明：平面PQEF和平面PQGH互相垂直；
（Ⅱ）证明：截面PQEF和截面PQGH面积之和是定值，
并求出这个值；
（Ⅲ）若
与平面PQEF所成的角为
，求与平面PQGH所成角的正弦值．
说明：本小题主要考查空间中的线面关系，面面关系，解三角形等基础知识，考查空间想象能力与逻辑思维能力。满分12分．
查看习题详情和答案>>（辽宁卷理19）如图，在棱长为1的正方体
中，AP=BQ=b（0<b<1），截面PQEF∥
，截面PQGH∥
．
（Ⅰ）证明：平面PQEF和平面PQGH互相垂直；
（Ⅱ）证明：截面PQEF和截面PQGH面积之和是定值，
并求出这个值；
（Ⅲ）若
与平面PQEF所成的角为
，求与平面PQGH所成角的正弦值．
说明：本小题主要考查空间中的线面关系，面面关系，解三角形等基础知识，考查空间想象能力与逻辑思维能力。满分12分．
查看习题详情和答案>>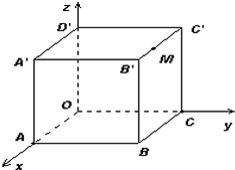
11、如图，棱长为3a正方体OABC-D'A'B'C'，点M在|B'C'|上，且|C'M|=2|MB'|，以O为坐标原点，建立如图空间直有坐标系，则点M的坐标为
（2a，3a，3a）
．
》的有5人；第二小组选《不等式选讲》的有2人，选《坐标系与参数方程》的有4人. 现从第一、第二两小组各任选2人分析得分情况.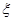
为选出的4个人中选《不等式选讲》的人数，求
,
,…
的10个零件，测量其直径（单位：cm），得到下面数据：
