摘要：4．向量与平面平行:如果表示向量的有向线段所在直线与平面平行或在平面内.我们就说向量平行于平面.记作∥.注意:向量∥与直线a∥的联系与区别. 共面向量:我们把平行于同一平面的向量叫做共面向量. 共面向量定理 如果两个向量.不共线.则向量与向量.共面的充要条件是存在实数对x.y.使① 注:与共线向量定理一样.此定理包含性质和判定两个方面. 推论:空间一点P位于平面MAB内的充要条件是存在有序实数对x.y.使 ④ 或对空间任一定点O.有⑤ 在平面MAB内.点P对应的实数对(x, y)是唯一的.①式叫做平面MAB的向量表示式. 又∵代入⑤.整理得 ⑥ 由于对于空间任意一点P.只要满足等式④.⑤.⑥之一(它们只是形式不同的同一等式).点P就在平面MAB内,对于平面MAB内的任意一点P.都满足等式④.⑤.⑥.所以等式④.⑤.⑥都是由不共线的两个向量.确定的空间平面的向量参数方程.也是M.A.B.P四点共面的充要条件.
网址：http://m.1010jiajiao.com/timu_id_4030663[举报]
平面直角坐标系内的向量都可以用一有序实数对唯一表示，这使我们想到可以用向量作为解析几何的研究工具．如图，设直线
l的倾斜角为α(α≠90°)．在l上任取两个不同的点
，
，不妨设向量
的方向是向上的，那么向量
的坐标是(
)．过原点作向量
，则点P的坐标是(
)，而且直线OP的倾斜角也是α．根据正切函数的定义得
，
这就是《数学
2》中已经得到的斜率公式．上述推导过程比《数学2》中的推导简捷．你能用向量作为工具讨论一下直线的有关问题吗？例如：(1)
过点
，平行于向量
的直线方程；
(2)
向量(A，B)与直线
的关系；
(3)
设直线
和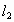
的方程分别是
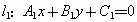
那么，
∥
，
的条件各是什么？如果它们相交，如何得到它们的夹角公式？
(4)
点
到直线
的距离公式如何推导？
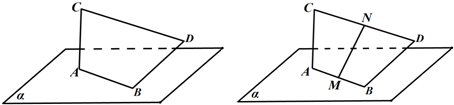
随着环保理念的深入，用建筑钢材余料创作城市雕塑逐渐流行．下图是其中一个抽象派雕塑的设计图．图中α表示水平地面，线段AB表示的钢管固定在α上；为了美感，需在焊接时保证：线段AC表示的钢管垂直于α，BD⊥AB，且保持BD与AC异面．
（1）若收集到的余料长度如下：AC=BD=24（单位长度），AB=7，CD=25，按现在手中的材料，求BD与α应成的角；
（2）设计师想在AB，CD中点M，N处再焊接一根连接管，然后挂一个与AC，BD同时平
行的平面板装饰物．但他担心此设计不一定能实现．请你替他打消疑虑：无论AB，CD多长，焊接角度怎样，一定存在一个过MN的平面与AC，BD同时平行（即证明向量
与
，
共面，写出证明过程）；
（3）如果事先能收集确定的材料只有AC=BD=24，请替设计师打消另一个疑虑：即MN要准备多长不用视AB，CD长度而定，只与θ有关（θ为设计的BD与α所成的角），写出MN与θ的关系式，并帮他算出无论如何设计MN都一定够用的长度．
查看习题详情和答案>>
（1）若收集到的余料长度如下：AC=BD=24（单位长度），AB=7，CD=25，按现在手中的材料，求BD与α应成的角；
（2）设计师想在AB，CD中点M，N处再焊接一根连接管，然后挂一个与AC，BD同时平
行的平面板装饰物．但他担心此设计不一定能实现．请你替他打消疑虑：无论AB，CD多长，焊接角度怎样，一定存在一个过MN的平面与AC，BD同时平行（即证明向量
| MN |
| AC |
| BD |
（3）如果事先能收集确定的材料只有AC=BD=24，请替设计师打消另一个疑虑：即MN要准备多长不用视AB，CD长度而定，只与θ有关（θ为设计的BD与α所成的角），写出MN与θ的关系式，并帮他算出无论如何设计MN都一定够用的长度．
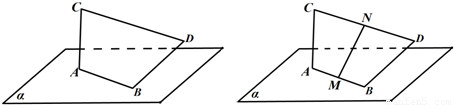
随着环保理念的深入，用建筑钢材余料创作城市雕塑逐渐流行．下图是其中一个抽象派雕塑的设计图．图中α表示水平地面，线段AB表示的钢管固定在α上；为了美感，需在焊接时保证：线段AC表示的钢管垂直于α，BD⊥AB，且保持BD与AC异面．
（1）若收集到的余料长度如下：AC=BD=24（单位长度），AB=7，CD=25，按现在手中的材料，求BD与α应成的角；
（2）设计师想在AB，CD中点M，N处再焊接一根连接管，然后挂一个与AC，BD同时平
行的平面板装饰物．但他担心此设计不一定能实现．请你替他打消疑虑：无论AB，CD多长，焊接角度怎样，一定存在一个过MN的平面与AC，BD同时平行（即证明向量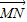
与
，
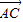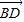共面，写出证明过程）；
（3）如果事先能收集确定的材料只有AC=BD=24，请替设计师打消另一个疑虑：即MN要准备多长不用视AB，CD长度而定，只与θ有关（θ为设计的BD与α所成的角），写出MN与θ的关系式，并帮他算出无论如何设计MN都一定够用的长度．
查看习题详情和答案>>
（1）若收集到的余料长度如下：AC=BD=24（单位长度），AB=7，CD=25，按现在手中的材料，求BD与α应成的角；
（2）设计师想在AB，CD中点M，N处再焊接一根连接管，然后挂一个与AC，BD同时平
行的平面板装饰物．但他担心此设计不一定能实现．请你替他打消疑虑：无论AB，CD多长，焊接角度怎样，一定存在一个过MN的平面与AC，BD同时平行（即证明向量
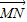与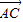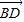，共面，写出证明过程）；（3）如果事先能收集确定的材料只有AC=BD=24，请替设计师打消另一个疑虑：即MN要准备多长不用视AB，CD长度而定，只与θ有关（θ为设计的BD与α所成的角），写出MN与θ的关系式，并帮他算出无论如何设计MN都一定够用的长度．
查看习题详情和答案>>
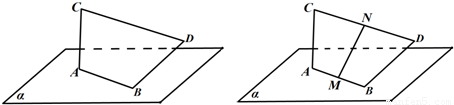
随着环保理念的深入，用建筑钢材余料创作城市雕塑逐渐流行．下图是其中一个抽象派雕塑的设计图．图中α表示水平地面，线段AB表示的钢管固定在α上；为了美感，需在焊接时保证：线段AC表示的钢管垂直于α，BD⊥AB，且保持BD与AC异面．
（1）若收集到的余料长度如下：AC=BD=24（单位长度），AB=7，CD=25，按现在手中的材料，求BD与α应成的角；
（2）设计师想在AB，CD中点M，N处再焊接一根连接管，然后挂一个与AC，BD同时平
行的平面板装饰物．但他担心此设计不一定能实现．请你替他打消疑虑：无论AB，CD多长，焊接角度怎样，一定存在一个过MN的平面与AC，BD同时平行（即证明向量
与
，
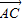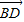共面，写出证明过程）；
（3）如果事先能收集确定的材料只有AC=BD=24，请替设计师打消另一个疑虑：即MN要准备多长不用视AB，CD长度而定，只与θ有关（θ为设计的BD与α所成的角），写出MN与θ的关系式，并帮他算出无论如何设计MN都一定够用的长度．
查看习题详情和答案>>
（1）若收集到的余料长度如下：AC=BD=24（单位长度），AB=7，CD=25，按现在手中的材料，求BD与α应成的角；
（2）设计师想在AB，CD中点M，N处再焊接一根连接管，然后挂一个与AC，BD同时平
行的平面板装饰物．但他担心此设计不一定能实现．请你替他打消疑虑：无论AB，CD多长，焊接角度怎样，一定存在一个过MN的平面与AC，BD同时平行（即证明向量
与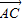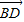，共面，写出证明过程）；（3）如果事先能收集确定的材料只有AC=BD=24，请替设计师打消另一个疑虑：即MN要准备多长不用视AB，CD长度而定，只与θ有关（θ为设计的BD与α所成的角），写出MN与θ的关系式，并帮他算出无论如何设计MN都一定够用的长度．
查看习题详情和答案>>