摘要：2．夹角 空间中的各种角包括异面直线所成的角.直线与平面所成的角和二面角.要理解各种角的概念定义和取值范围.其范围依次为0°.90°.[0°.90°]和[0°.180°]. (1)两条异面直线所成的角 求法:1先通过其中一条直线或者两条直线的平移.找出这两条异面直线所成的角.然后通过解三角形去求得,2通过两条异面直线的方向量所成的角来求得.但是注意到异面直线所成角得范围是.向量所成的角范围是.如果求出的是钝角.要注意转化成相应的锐角. (2)直线和平面所成的角 求法:“一找二证三求 .三步都必须要清楚地写出来.除特殊位置外.主要是指平面的斜线与平面所成的角.根据定义采用“射影转化法 . (3)二面角的度量是通过其平面角来实现的 解决二面角的问题往往是从作出其平面角的图形入手.所以作二面角的平面角就成为解题的关键.通常的作法有:利用三垂线定理或逆定理,(Ⅲ)自空间一点作棱垂直的垂面.截二面角得两条射线所成的角.俗称垂面法．此外.当作二面角的平面角有困难时.可用射影面积法解之.cos ＝.其中S 为斜面面积.S′为射影面积. 为斜面与射影面所成的二面角.
网址：http://m.1010jiajiao.com/timu_id_4030341[举报]
12、给定下列四个命题：
（1）给定空间中的直线l及平面α，“直线l与平面α内无数条直线垂直”是“直线l与平面α垂直”的充分不必要条件；
（2）已知α，β表示两个不同的平面，m为平面α内的一条直线，则“α⊥β”是“m⊥β”的必要不充分条件；
（3）已知m，n是两条不同的直线，α，β是两个不同的平面，若m∥α，n∥β，m⊥n，则α⊥β；
（4）在三棱柱ABC-A1B1C1中，各棱长相等，侧棱垂直于底面，点D是侧面BB1C1C的中心，则AD与平面BB1C1C所成角的大小是60°．
上述命题中，真命题的序号是（ ）
（1）给定空间中的直线l及平面α，“直线l与平面α内无数条直线垂直”是“直线l与平面α垂直”的充分不必要条件；
（2）已知α，β表示两个不同的平面，m为平面α内的一条直线，则“α⊥β”是“m⊥β”的必要不充分条件；
（3）已知m，n是两条不同的直线，α，β是两个不同的平面，若m∥α，n∥β，m⊥n，则α⊥β；
（4）在三棱柱ABC-A1B1C1中，各棱长相等，侧棱垂直于底面，点D是侧面BB1C1C的中心，则AD与平面BB1C1C所成角的大小是60°．
上述命题中，真命题的序号是（ ）
查看习题详情和答案>>
（2009•黄浦区一模）在空间中，给出下列4个命题（其中a、b、c表示直线，β表示平面），则正确命题的序号是（ ）
（1）三个点确定一个平面；
（2）若a∥c，b∥c，则a∥b；
（3）在空间中，若角θ1与角θ2的两边分别平行，则θ1=θ2；
（4）若a⊥b，a⊥c，b、c?β，则α⊥β．
（1）三个点确定一个平面；
（2）若a∥c，b∥c，则a∥b；
（3）在空间中，若角θ1与角θ2的两边分别平行，则θ1=θ2；
（4）若a⊥b，a⊥c，b、c?β，则α⊥β．
查看习题详情和答案>>
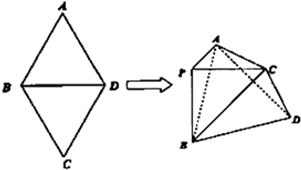如图，菱形ABCD中，∠A=60°，把菱形ABCD沿对角线BD折成二面角A-BD-C，AC=BD，空间中的点P满足PA、PB、PC两两垂直，则下列命题中错误的是（ ）