摘要：1．平面的基本性质与推论 借助长方体模型.在直观认识和理解空间点.线.面的位置关系的基础上.抽象出空间线.面位置关系的定义.并了解如下可以作为推理依据的公理和定理: ◆公理1:如果一条直线上的两点在一个平面内.那么这条直线在此平面内, ◆公理2:过不在一条直线上的三点.有且只有一个平面, ◆公理3:如果两个不重合的平面有一个公共点.那么它们有且只有一条过该点的公共直线, ◆公理4:平行于同一条直线的两条直线平行, ◆定理:空间中如果两个角的两条边分别对应平行.那么这两个角相等或互补.
网址：http://m.1010jiajiao.com/timu_id_4030313[举报]
下列命题中，正确命题的个数为( )
①平面的基本性质1可用集合符号叙述为：若A∈l，B∈l，且A∈α，B∈α，则必有l∈α；
②四边形的两条对角线必相交于一点；
③用平行四边形表示的平面，以平行四边形的四条边作为平面的边界线；
④平行四边形是平面图形．
A．1个 B．2个 C．3个 D．4个
查看习题详情和答案>>
已知离心率为
的椭圆C1的顶点A1，A2恰好是双曲线
-y2=1的左右焦点，点P是椭圆上不同于A1，A2的任意一点，设直线PA1，PA2的斜率分别为k1，k2．
（Ⅰ）求椭圆C1的标准方程；
（Ⅱ）试判断k1•k2的值是否与点P的位置有关，并证明你的结论；
（Ⅲ）当k1=
时，圆C2：x2+y2-2mx=0被直线PA2截得弦长为
，求实数m的值．
设计意图：考察直线上两点的斜率公式、直线与圆相交、垂径定理、双曲线与椭圆的几何性质等知识，考察学生用待定系数法求椭圆方程等解析几何的基本思想与运算能力、探究能力和推理能力．第（Ⅱ）改编自人教社选修2-1教材P39例3． 查看习题详情和答案>>
| ||
| 2 |
| x2 |
| 3 |
（Ⅰ）求椭圆C1的标准方程；
（Ⅱ）试判断k1•k2的值是否与点P的位置有关，并证明你的结论；
（Ⅲ）当k1=
| 1 |
| 2 |
4
| ||
| 5 |
设计意图：考察直线上两点的斜率公式、直线与圆相交、垂径定理、双曲线与椭圆的几何性质等知识，考察学生用待定系数法求椭圆方程等解析几何的基本思想与运算能力、探究能力和推理能力．第（Ⅱ）改编自人教社选修2-1教材P39例3． 查看习题详情和答案>>
已知离心率为
的椭圆C1的顶点A1，A2恰好是双曲线
的左右焦点，点P是椭圆上不同于A1，A2的任意一点，设直线PA1，PA2的斜率分别为k1，k2．
（Ⅰ）求椭圆C1的标准方程；
（Ⅱ）试判断k1•k2的值是否与点P的位置有关，并证明你的结论；
（Ⅲ）当
时，圆C2：x2+y2-2mx=0被直线PA2截得弦长为
，求实数m的值．
设计意图：考察直线上两点的斜率公式、直线与圆相交、垂径定理、双曲线与椭圆的几何性质等知识，考察学生用待定系数法求椭圆方程等解析几何的基本思想与运算能力、探究能力和推理能力．第（Ⅱ）改编自人教社选修2-1教材P39例3．
查看习题详情和答案>>
的椭圆C1的顶点A1，A2恰好是双曲线的左右焦点，点P是椭圆上不同于A1，A2的任意一点，设直线PA1，PA2的斜率分别为k1，k2．（Ⅰ）求椭圆C1的标准方程；
（Ⅱ）试判断k1•k2的值是否与点P的位置有关，并证明你的结论；
（Ⅲ）当
时，圆C2：x2+y2-2mx=0被直线PA2截得弦长为，求实数m的值．设计意图：考察直线上两点的斜率公式、直线与圆相交、垂径定理、双曲线与椭圆的几何性质等知识，考察学生用待定系数法求椭圆方程等解析几何的基本思想与运算能力、探究能力和推理能力．第（Ⅱ）改编自人教社选修2-1教材P39例3．
查看习题详情和答案>>
已知离心率为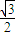
的椭圆C1的顶点A1，A2恰好是双曲线
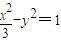的左右焦点，点P是椭圆上不同于A1，A2的任意一点，设直线PA1，PA2的斜率分别为k1，k2．
（Ⅰ）求椭圆C1的标准方程；
（Ⅱ）试判断k1•k2的值是否与点P的位置有关，并证明你的结论；
（Ⅲ）当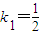
时，圆C2：x2+y2-2mx=0被直线PA2截得弦长为
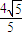，求实数m的值．
设计意图：考察直线上两点的斜率公式、直线与圆相交、垂径定理、双曲线与椭圆的几何性质等知识，考察学生用待定系数法求椭圆方程等解析几何的基本思想与运算能力、探究能力和推理能力．第（Ⅱ）改编自人教社选修2-1教材P39例3．
查看习题详情和答案>>
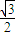的椭圆C1的顶点A1，A2恰好是双曲线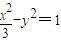的左右焦点，点P是椭圆上不同于A1，A2的任意一点，设直线PA1，PA2的斜率分别为k1，k2．（Ⅰ）求椭圆C1的标准方程；
（Ⅱ）试判断k1•k2的值是否与点P的位置有关，并证明你的结论；
（Ⅲ）当
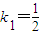时，圆C2：x2+y2-2mx=0被直线PA2截得弦长为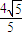，求实数m的值．设计意图：考察直线上两点的斜率公式、直线与圆相交、垂径定理、双曲线与椭圆的几何性质等知识，考察学生用待定系数法求椭圆方程等解析几何的基本思想与运算能力、探究能力和推理能力．第（Ⅱ）改编自人教社选修2-1教材P39例3．
查看习题详情和答案>>
[番茄花园1] 本题共有3个小题，第1小题满分3分，第2小题满分5分，第3小题满分10分。
若实数
、
、
满足
，则称比远离.
（1）若
比1远离0，求的取值范围；
（2）对任意两个不相等的正数
、
，证明：
比
远离
；
（3）已知函数
的定义域
.任取
，等于
和
中远离0的那个值.写出函数的解析式，并指出它的基本性质（结论不要求证明）.
23本题共有3个小题，第1小题满分3分，第2小题满分6分，第3小题满分9分.
已知椭圆
的方程为
，点P的坐标为（-a，b）.
（1）若直角坐标平面上的点M、A(0,-b)，B(a，0)满足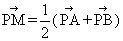
,求点
的坐标；
（2）设直线
交椭圆于
、
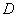两点，交直线
于点
.若
，证明：为
的中点；
（3）对于椭圆上的点Q（a cosθ，b sinθ）（0＜θ＜π），如果椭圆上存在不同的两个交点
、
满足
,写出求作点、的步骤，并求出使、存在的θ的取值范围.
[番茄花园1]22.
查看习题详情和答案>>