摘要：3．二次函数的基本性质 (1)二次函数的三种表示法:y=ax2+bx+c,y=a(x-x1)(x-x2),y=a(x-x0)2+n. (2)当a>0.f(x)在区间［p.q］上的最大值M.最小值m.令x0= (p+q). 若-<p.则f(p)=m.f(q)=M, 若p≤-<x0.则f(-)=m.f(q)=M, 若x0≤-<q.则f(p)=M.f(-)=m, 若-≥q.则f(p)=M.f(q)=m. (3)二次方程f(x)=ax2+bx+c=0的实根分布及条件. ①方程f(x)=0的两根中一根比r大.另一根比r小a·f(r)<0, ②二次方程f(x)=0的两根都大于r ③二次方程f(x)=0在区间(p.q)内有两根 ④二次方程f(x)=0在区间(p.q)内只有一根f(p)·f(q)<0.或f(p)=0或f(q)=0检验另一根若在(p.q)内成立.
网址：http://m.1010jiajiao.com/timu_id_4030277[举报]
根据二次函数的性质填空：
（1）一般式：y=ax2+bx+c（a≠0）；对称轴方程是 ；顶点为 ；
（2）两点式：y=a（x-x1）（x-x2）；对称轴方程是 ；与x轴的交点为 ；
（3）顶点式：y=a（x-k）2+h；对称轴方程是 ；顶点为 ．
查看习题详情和答案>>
（1）一般式：y=ax2+bx+c（a≠0）；对称轴方程是
（2）两点式：y=a（x-x1）（x-x2）；对称轴方程是
（3）顶点式：y=a（x-k）2+h；对称轴方程是
在函数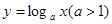
的图象上有
、
、
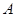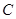三点，横坐标分别为
其中
．
⑴求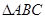
的面积
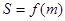的表达式；
⑵求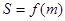的值域．
【解析】由题意利用分割可先表示三角形ABC的面积，然后应用对数运算性质及二次函数的性质求解函数的最大值，属于知识的简单综合.
查看习题详情和答案>>
，利用二次函数的性质，试求当a取何值时，
达到最小值．
，试利用最小二乘法和二次函数的性质，推导这n个点的线性回归方程．