摘要:如图所示.倾斜角为的直线经过抛物线y2=8x的焦点F.且与抛物线交于A.B两点. (1)求抛物线焦点F的坐标及准线l的方程, (2)若为锐角.作线段AB的垂直平分线m交x轴于点P.证明|FP|-|FP|cos2为定值. 并求此定值. (1)解 由已知得2 p=8,∴=2, ∴抛物线的焦点坐标为F(2.0).准线方程为x=-2. (2)证明 设A(xA.yA).B(xB.yB).直线AB的斜率为k=tan,则直线方程为y=k(x-2), 将此式代入y2=8x,得k2x2-4(k2+2)x+4k2=0, 故xA+xB=, 记直线m与AB的交点为E(xE,yE).则 xE==,yE=k(xE-2)=, 故直线m的方程为y-=-, 令y=0,得点P的横坐标xP=+4, 故|FP|=xP-2==, ∴|FP|-|FP|cos2=(1-cos2)==8,为定值.
网址:http://m.1010jiajiao.com/timu_id_4028774[举报]
如图所示,倾斜角为![]() 的直线经过抛物线y2=8x的焦点F,且与抛物线交于A、B两点.
的直线经过抛物线y2=8x的焦点F,且与抛物线交于A、B两点.
(1)求抛物线焦点F的坐标及准线l的方程;
(2)若![]() 为锐角,作线段AB的垂直平分线m交x轴于点P,证明|FP|-|FP|cos2
为锐角,作线段AB的垂直平分线m交x轴于点P,证明|FP|-|FP|cos2![]() 为定值,
为定值,
并求此定值.

如图所示,倾斜角为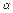 的直线经过抛物线y2=8x的焦点F,且与抛物线交于A、B两点.
的直线经过抛物线y2=8x的焦点F,且与抛物线交于A、B两点.
(1)求抛物线焦点F的坐标及准线l的方程;
(2)若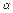 为锐角,作线段AB的垂直平分线m交x轴于点P,证明|FP|-|FP|cos2
为锐角,作线段AB的垂直平分线m交x轴于点P,证明|FP|-|FP|cos2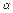 为定值,
为定值,
并求此定值.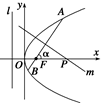
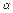 的直线经过抛物线y2=8x的焦点F,且与抛物线交于A、B两点.
的直线经过抛物线y2=8x的焦点F,且与抛物线交于A、B两点.(1)求抛物线焦点F的坐标及准线l的方程;
(2)若
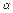 为锐角,作线段AB的垂直平分线m交x轴于点P,证明|FP|-|FP|cos2
为锐角,作线段AB的垂直平分线m交x轴于点P,证明|FP|-|FP|cos2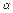 为定值,
为定值, 并求此定值.

(本小题满分13分)
如图所示,倾斜角为![]() 的直线经过抛物线
的直线经过抛物线![]() 的焦点F,且与抛物线交于A、B两点.
的焦点F,且与抛物线交于A、B两点.
 (1)求抛物线焦点F的坐标及准线l的方程;中国教考资源网
(1)求抛物线焦点F的坐标及准线l的方程;中国教考资源网
(2)若![]() 为锐角,作线段AB的垂直平分线m交x轴于点P,证明|FP|-|FP|cos2
为锐角,作线段AB的垂直平分线m交x轴于点P,证明|FP|-|FP|cos2![]() 为定值,并求此定值.
为定值,并求此定值.
 (1)求抛物线焦点F的坐标及准线l的方程;中国教考资源网
(1)求抛物线焦点F的坐标及准线l的方程;中国教考资源网 如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为
如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为