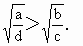摘要：掌握不等式的性质及其证明.能正确使用这些性质解决一些简单问题
网址：http://m.1010jiajiao.com/timu_id_4028142[举报]
关于不等式的性质：
①a＞b?a+c＞b+c；②a＞b，b＞c?a＞c；③a＞b，c＞0?ac＞bc；④a＞b，c＜0?ac＜bc；
⑤a＞b，c＞d?a+c＞b+d；⑥a＞b＞0，c＞d＞0?ac＞bd；⑦a＞b＞0，n∈N*?an＞bn；
⑧a＞b＞0，n∈N，n＞1?
＞
．其中正确的有 （填序号）．
查看习题详情和答案>>
①a＞b?a+c＞b+c；②a＞b，b＞c?a＞c；③a＞b，c＞0?ac＞bc；④a＞b，c＜0?ac＜bc；
⑤a＞b，c＞d?a+c＞b+d；⑥a＞b＞0，c＞d＞0?ac＞bd；⑦a＞b＞0，n∈N*?an＞bn；
⑧a＞b＞0，n∈N，n＞1?
| n | a |
| n | b |
.若
<
<0,则下列不等式:①a+b<ab；②|a|>|b|；③a<b；④
+
>2.正确的不等式有
A.1个 B.2个 C.3个 D.4个
本题主要考查不等式的性质及均值不等式的适用条件.
查看习题详情和答案>>
关于不等式的性质：
①a＞b?a+c＞b+c；②a＞b，b＞c⇒a＞c；③a＞b，c＞0⇒ac＞bc；④a＞b，c＜0⇒ac＜bc；
⑤a＞b，c＞d⇒a+c＞b+d；⑥a＞b＞0，c＞d＞0⇒ac＞bd；⑦a＞b＞0，n∈N*⇒an＞bn；
⑧
．其中正确的有 （填序号）．
查看习题详情和答案>>
①a＞b?a+c＞b+c；②a＞b，b＞c⇒a＞c；③a＞b，c＞0⇒ac＞bc；④a＞b，c＜0⇒ac＜bc；
⑤a＞b，c＞d⇒a+c＞b+d；⑥a＞b＞0，c＞d＞0⇒ac＞bd；⑦a＞b＞0，n∈N*⇒an＞bn；
⑧
．其中正确的有 （填序号）．
查看习题详情和答案>>
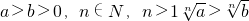．其中正确的有________（填序号）．