摘要：3. 0.03. 0.003.- 各项的和. 例2.将无限循环小数化为分数.
网址：http://m.1010jiajiao.com/timu_id_4027271[举报]
24、已知下表为定义域为R的函数f（x）=ax3+cx+d若干自变量取值及其对应函数值，为便于研究，相关函数值非整数值时，取值精确到0.01．
根据表中数据解答下列问题：
（1）函数y=f（x）在区间[0.55，0.6]上是否存在零点，写出判断并说明理由；
（2）证明：函数y=f（x）在区间（-∞，-0.35]单调递减．
查看习题详情和答案>>
| x | 3.27 | 1.57 | -0.61 | -0.59 | 0.26 | 0.42 | -0.35 | -0.56 | 0 | 4.25 |
| y | -101.63 | -10.04 | 0.07 | 0.03 | 0.21 | 0.20 | -0.22 | -0.03 | 0 | -226.05 |
（1）函数y=f（x）在区间[0.55，0.6]上是否存在零点，写出判断并说明理由；
（2）证明：函数y=f（x）在区间（-∞，-0.35]单调递减．
两个气象台同时作天气预报，如果他们与预报准确的概率分别为0.8与0.9，那么在一次预报中，两个气象台都没预报准确的概率为（ ）
A.0.72 B.0.3
C.0.02 D.0.03
查看习题详情和答案>>设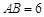
，在线段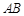
上任取两点C,D（端点
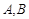除外），将线段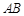分成三条线段AC,CD,DB.
（1）若分成的三条线段的长度均为正整数，求这三条线段可以构成三角形（称事件A）的概率；
（2）若分成的三条线段的长度均为正实数，求这三条线段可以构成三角形（称事件B）的概率；
（3）根据以下用计算机所产生的20组随机数，试用随机数摸拟的方法，来近似计算（Ⅱ）中事件B的概率.
20组随机数如下：
|
|
1组 |
2组 |
3组 |
4组 |
5组 |
6组 |
7组 |
8组 |
9组 |
10组 |
|
X |
0.52 |
0.36 |
0.58 |
0.73 |
0.41 |
0. 6 |
0.05 |
0.32 |
0.38 |
0.73 |
|
Y |
0.76 |
0.39 |
0.37 |
0.01 |
0.04 |
0.28 |
0.03 |
0.15 |
0.14 |
0.86 |
|
|
11组 |
12组 |
13组 |
14组 |
15组 |
16组 |
17组 |
18组 |
19组 |
20组 |
|
X |
0.67 |
0.47 |
0.58 |
0.21 |
0.54 |
0. 64 |
0.36 |
0.35 |
0.95 |
0.14 |
|
Y |
0.41 |
0.54 |
0.51 |
0.37 |
0.31 |
0.23 |
0.56 |
0.89 |
0.17 |
0.03 |
（X是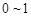
之间的均匀随机数，Y也是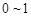之间的均匀随机数）
查看习题详情和答案>>
已知下表为函数f（x）=ax3+cx+d部分自变量取值及其对应函数值，为便于研究，相关函数值非整数值时，取值精确到0.01．
下列关于函数f（x）的叙述：
（1）f（x）为奇函数； （2）f（x）在[0.55，0.6]上必有零点
（3）f（x）在（-∞，-0.35]上单调递减； （4）a＜0
其中所有正确命题的个数是（ ）
A．4
B．3
C．2
D．1
查看习题详情和答案>>
| x | 3.27 | 1.57 | -0.61 | -0.59 | 0.26 | 0.42 | -0.35 | -0.56 | 4.25 | |
| y | -101.63 | -10.04 | 0.07 | 0.026 | 0.21 | 0.20 | -0.22 | -0.03 | -226.05 |
（1）f（x）为奇函数； （2）f（x）在[0.55，0.6]上必有零点
（3）f（x）在（-∞，-0.35]上单调递减； （4）a＜0
其中所有正确命题的个数是（ ）
A．4
B．3
C．2
D．1
查看习题详情和答案>>