摘要: 解:·································································································· 3分 或····································································································· 5分 .······································································································· 6分
网址:http://m.1010jiajiao.com/timu_id_4025735[举报]
解:(1)由题意知,当![]() 、
、![]() 运动到
运动到![]() 秒时,如图①,过
秒时,如图①,过![]() 作
作![]() 交
交![]() 于
于![]() 点,则四边形
点,则四边形![]() 是平行四边形.
是平行四边形.
∵![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∴ ![]() .解得
.解得![]() . 5分
. 5分
(2)分三种情况讨论:
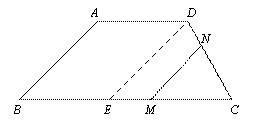
① 当![]() 时,如图②作
时,如图②作![]() 交
交![]() 于
于![]() ,则有
,则有![]() 即.
即.
 ∵
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得![]() . 6分
. 6分
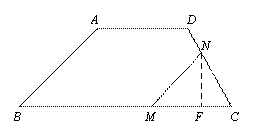
② 当![]() 时,如图③,过
时,如图③,过![]() 作
作![]() 于H.
于H.
 则
则![]() ,
,
∴![]() .
.
∴![]() .7分
.7分
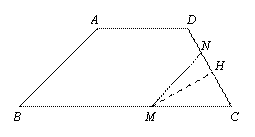
③ 当![]() 时,如图④.
时,如图④.
则![]() .
.
![]() . -------------------------------------8分
. -------------------------------------8分
综上所述,当![]() 、
、![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
解下列分式方程或不等式(组),并将不等式(组)的解集表示在数轴上:
(1)3x-(x+2)>0;(2)
(3)
=
;(4)
=
-
.
查看习题详情和答案>>
(1)3x-(x+2)>0;(2)
|
(3)
| 4 |
| x+1 |
| 3 |
| x |
| x-2 |
| x+2 |
| 16 |
| x2-4 |
| x+2 |
| 2-x |
解决下面问题:
如图,在△ABC中,∠A是锐角,点D,E分别在AB,AC上,且∠DCB=∠EBC=
∠A,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
小新同学是这样思考的:
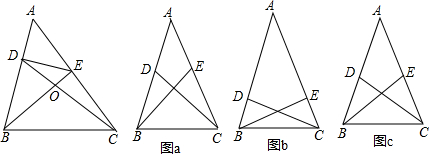
在平时的学习中,有这样的经验:假如△ABC是等腰三角形,那么在给定一组对应条件,如图a,BE,CD分别是两底角的平分线(或者如图b,BE,CD分别是两条腰的高线,或者如图c,BE,CD分别是两条腰的中线)时,依据图形的轴对称性,利用全等三角形和等腰三角形的有关知识就可证得更多相等的线段或相等的角.这个问题也许可以通过添加辅助线构造轴对称图形来解决.请参考小新同学的思路,解决上面这个问题.
查看习题详情和答案>>
如图,在△ABC中,∠A是锐角,点D,E分别在AB,AC上,且∠DCB=∠EBC=
| 1 | 2 |

小新同学是这样思考的:
在平时的学习中,有这样的经验:假如△ABC是等腰三角形,那么在给定一组对应条件,如图a,BE,CD分别是两底角的平分线(或者如图b,BE,CD分别是两条腰的高线,或者如图c,BE,CD分别是两条腰的中线)时,依据图形的轴对称性,利用全等三角形和等腰三角形的有关知识就可证得更多相等的线段或相等的角.这个问题也许可以通过添加辅助线构造轴对称图形来解决.请参考小新同学的思路,解决上面这个问题.
解决下面问题:
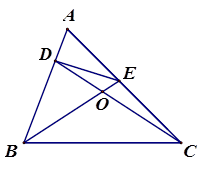
如图,在△ABC中,∠A是锐角,点D,E分别在AB,AC上,且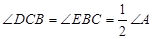 ,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
小新同学是这样思考的:
在平时的学习中,有这样的经验:假如△ABC是等腰三角形,那么在给定一组对应条件,如图a,BE,CD分别是两底角的平分线(或者如图b,BE,CD分别是两条腰的高线,或者如图c,BE,CD分别是两条腰的中线)时,依据图形的轴对称性,利用全等三角形和等腰三角形的有关知识就可证得更多相等的线段或相等的角.这个问题也许可以通过添加辅助线构造轴对称图形来解决.
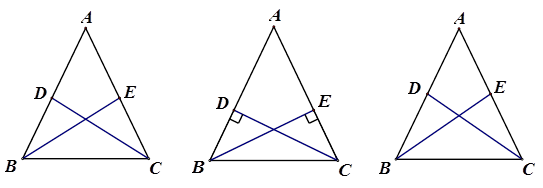
图a 图b 图c
请参考小新同学的思路,解决上面这个问题..
如图,在△ABC中,∠A是锐角,点D,E分别在AB,AC上,且
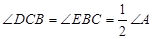 ,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
小新同学是这样思考的:
在平时的学习中,有这样的经验:假如△ABC是等腰三角形,那么在给定一组对应条件,如图a,BE,CD分别是两底角的平分线(或者如图b,BE,CD分别是两条腰的高线,或者如图c,BE,CD分别是两条腰的中线)时,依据图形的轴对称性,利用全等三角形和等腰三角形的有关知识就可证得更多相等的线段或相等的角.这个问题也许可以通过添加辅助线构造轴对称图形来解决.
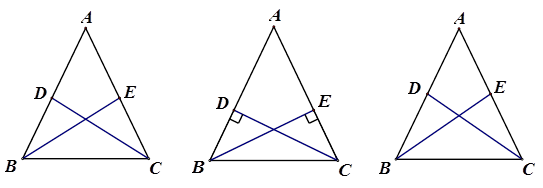
图a 图b 图c
请参考小新同学的思路,解决上面这个问题..
解决下面问题:
如图,在△ABC中,∠A是锐角,点D,E分别在AB,AC上,且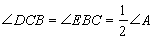 ,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
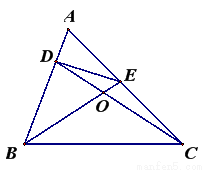
小新同学是这样思考的:
在平时的学习中,有这样的经验:假如△ABC是等腰三角形,那么在给定一组对应条件,如图a,BE,CD分别是两底角的平分线(或者如图b,BE,CD分别是两条腰的高线,或者如图c,BE,CD分别是两条腰的中线)时,依据图形的轴对称性,利用全等三角形和等腰三角形的有关知识就可证得更多相等的线段或相等的角.这个问题也许可以通过添加辅助线构造轴对称图形来解决.
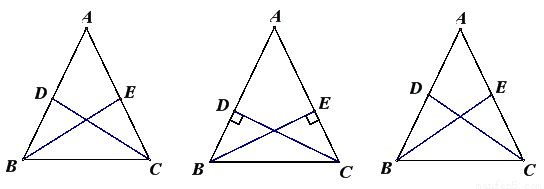
图a 图b 图c
请参考小新同学的思路,解决上面这个问题..
查看习题详情和答案>>