摘要:例1 等于( ) A.-1 B.0 C.1 D.不能确定 答案: D. 因为当||<1即a<时.=0. 当||>1时.不存在. 当=1即a=时.=1 当=-1时.也不存在. 例2 已知|a|>|b|.且 (n∈N*).那么a的取值范围是( ) A.a<-1 B.-1<a<0 C.a>1 D.a>1或-1<a<0 答案:D.左边= 右边= ∵|a|>|b|.∴||<1. ∴()n=0 ∴不等式变为<a.解不等式得a>1或-1<a<0. 例1.例2在数列极限中.极限qn=0要注意这里|q|<1.这个极限很重要. 例3 =8.试确定a.b的值. 分析:因为x→2时.分母x-2用代入法时等于0.所以应该用因式分解法.则分母中应该也有x-2这个因子.只要将公因式x-2消去.用代入法求极限.再根据极限是8.就可以求a.b了. 解: ∴由题意 例4 求 分析:首先.当x=0代入分母时分母为零.所以可能要用因式分解法.但分子分母都是根式.所以要分别对分子分母有理化法. 解:
网址:http://m.1010jiajiao.com/timu_id_4025056[举报]
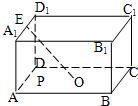 例2:如图,在长方体ABCD-A1B1C1D1中,AB=AD=2AA1=4,点O是底面ABCD的中心,点E是A1D1的中点,点P是底面ABCD上的动点,且到直线OE的距离等于1,对于点P的轨迹,下列说法正确的是( )
例2:如图,在长方体ABCD-A1B1C1D1中,AB=AD=2AA1=4,点O是底面ABCD的中心,点E是A1D1的中点,点P是底面ABCD上的动点,且到直线OE的距离等于1,对于点P的轨迹,下列说法正确的是( )A、离心率为
| ||||
B、离心率为
| ||||
| C、一段抛物线 | ||||
| D、半径等于1的圆 |