摘要: 三角形中的有关公式: (1)内角和定理:三角形三角和为.这是三角形中三角函数问题的特殊性.解题可不能忘记!任意两角和与第三个角总互补.任意两半角和与第三个角的半角总互余.锐角三角形三内角都是锐角三内角的余弦值为正值任两角和都是钝角任意两边的平方和大于第三边的平方. (2)正弦定理:(R为三角形外接圆的半径).注意:①正弦定理的一些变式:, ,,②已知三角形两边一对角.求解三角形时.若运用正弦定理.则务必注意可能有两解. (3)余弦定理:等.常选用余弦定理鉴定三角形的形状. (4)面积公式:(其中为三角形内切圆半径).如中.若.判断的形状. 特别提醒:(1)求解三角形中的问题时.一定要注意这个特殊性:,(2)求解三角形中含有边角混合关系的问题时.常运用正弦定理.余弦定理实现边角互化.如(1)中.A.B的对边分别是.且.那么满足条件的 A. 有一个解 B.有两个解 C.无解 D.不能确定在中.A>B是成立的 条件在中. .则= (答:),(4)在中.分别是角A.B.C所对的边.若.则= (答:),(5)在中.若其面积.则= (答:),(6)在中..这个三角形的面积为.则外接圆的直径是 (答:),(7)在△ABC中.a.b.c是角A.B.C的对边.= .的最大值为 (答:),(8)在△ABC中AB=1.BC=2.则角C的取值范围是 (答:),(9)设O是锐角三角形ABC的外心.若.且的面积满足关系式.求(答:).
网址:http://m.1010jiajiao.com/timu_id_4023581[举报]
在△ABC中,角A,B,C所对的边分别为a,b,c, △ABC的面积
S=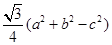
(1)求角C的大小
(2)若c=1,求△ABC周长L的取值范围
【解析】本试题主要是考查了解三角形中的面积公式和两个定理的运用。
查看习题详情和答案>>
 如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,AC=2
如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,AC=2| 3 |
(Ⅰ)求证SA⊥SC;
(Ⅱ)在平面几何中,推导三角形内切圆的半径公式r=
| 2S |
| l |
①以内切圆的圆心O为顶点,将三角形ABC分割成三个小三角形:△OAB,△OAC,△OB
 C.
C.②设△ABC三边长分别为a,b,c.由S△ABC=S△OBC+S△OAC+S△OAB,
得S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2S |
| l |
类比上述方法,请给出四面体内切球半径的计算公式(不要求说明类比过程),并利用该公式求出三棱锥S-ABC内切球的半径. 查看习题详情和答案>>
阅读下面所给材料:已知数列{an},a1=2,an=3an-1+2,求数列的通项an.
解:令an=an-1=x,则有x=3x+2,所以x=-1,故原递推式an=3an-1+2可转化为:
an+1=3(an-1+1),因此数列{an+1}是首项为a1+1,公比为3的等比数列.
根据上述材料所给出提示,解答下列问题:
已知数列{an},a1=1,an=3an-1+4,
(1)求数列的通项an;并用解析几何中的有关思想方法来解释其原理;
(2)若记Sn=
,求
Sn;
(3)若数列{bn}满足:b1=10,bn+1=100bn3,利用所学过的知识,把问题转化为可以用阅读材料的提示,求出解数列{bn}的通项公式bn. 查看习题详情和答案>>
解:令an=an-1=x,则有x=3x+2,所以x=-1,故原递推式an=3an-1+2可转化为:
an+1=3(an-1+1),因此数列{an+1}是首项为a1+1,公比为3的等比数列.
根据上述材料所给出提示,解答下列问题:
已知数列{an},a1=1,an=3an-1+4,
(1)求数列的通项an;并用解析几何中的有关思想方法来解释其原理;
(2)若记Sn=
| n |
 |
| k=1 |
| 1 |
| lg(ak+2)lg(ak+1+2) |
| lim |
| n→∞ |
(3)若数列{bn}满足:b1=10,bn+1=100bn3,利用所学过的知识,把问题转化为可以用阅读材料的提示,求出解数列{bn}的通项公式bn. 查看习题详情和答案>>