摘要:正弦函数.余弦函数的性质: (1)定义域:都是R. (2)值域:都是.对.当时.取最大值1,当时.取最小值-1,对.当时.取最大值1.当时.取最小值-1.如(1)若函数的最大值为.最小值为.则 ._(答:或),(2)函数()的值域是 若.则的最大值和最小值分别是 . 函数的最小值是 .此时= (答:2,),(5)己知.求的变化范围(答:),(6)若.求的最大.最小值(答:.).特别提醒:在解含有正余弦函数的问题时.你深入挖掘正余弦函数的有界性了吗? (3)周期性:①.的最小正周期都是2,②和的最小正周期都是.如(1)若.则= 函数 的最小正周期为 (答:),(3) 设函数.若对任意都有成立.则的最小值为 (4)奇偶性与对称性:正弦函数是奇函数.对称中心是.对称轴是直线,余弦函数是偶函数.对称中心是.对称轴是直线弦型函数的对称轴为过最高点或最低点且垂直于轴的直线.对称中心为图象与轴的交点).如(1)函数的奇偶性是 已知函数为常数).且.则 函数的图象的对称中心和对称轴分别是 . (答:.),(4)已知为偶函数.求的值.(答:) (5)单调性:上单调递增.在单调递减,在上单调递减.在上单调递增.特别提醒.别忘了!
网址:http://m.1010jiajiao.com/timu_id_4023578[举报]
 ,
, ”为双曲正弦函数,“
”为双曲正弦函数,“ ,
, 、
、 等.请你再写出一个类似的性质:
等.请你再写出一个类似的性质: .
. ,
, ”为双曲正弦函数,“
”为双曲正弦函数,“ ,
,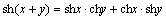 、
、 等.请你再写出一个类似的性质:
等.请你再写出一个类似的性质: .
.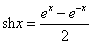 ,
, ”为双曲正弦函数,“
”为双曲正弦函数,“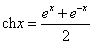 ,
,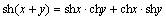 、
、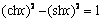 等.请你再写出一个类似的性质:
等.请你再写出一个类似的性质: .
.