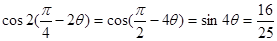摘要: 三角函数的化简.计算.证明的恒等变形的基本思路是:一角二名三结构.即首先观察角与角之间的关系.注意角的一些常用变式.角的变换是三角函数变换的核心!第二看函数名称之间的关系.通常“切化弦 ,第三观察代数式的结构特点.基本的技巧有: (1)巧变角(已知角与特殊角的变换.已知角与目标角的变换.角与其倍角的变换.两角与其和差角的变换. 如....等).如(1)已知..那么的值是 (答:),(2)已知.且..求的值(答:),(3)已知为锐角...则与的函数关系为 (答:) (2)三角函数名互化求值已知.求的值(答:) (3)公式变形使用(.如(1)已知A.B为锐角.且满足.则= (答:),(2)设中...则此三角形是 三角形 (4)三角函数次数的降升(降幂公式:.与升幂公式:.).如(1)若.化简为 (答:),(2)函数 的单调递增区间为 (答:) (5)式子结构的转化(对角.函数名.式子结构化同).如(1) (答:),(2)求证:,(3)化简:(答:) (6)常值变换主要指“1 的变换( 等).如已知.求(答:). (7)正余弦“三兄妹— 的内存联系--“知一求二 .如(1)若 .则 (答:).特别提醒:这里,(2)若.求的值.(答:),(3)已知.试用表示的值(答:).
网址:http://m.1010jiajiao.com/timu_id_4023575[举报]
已知函数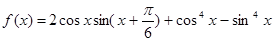
(1)求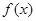 的最小正周期;
的最小正周期;
(2)若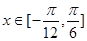 ,求
,求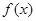 的最大值、最小值及相应的x的值。
的最大值、最小值及相应的x的值。
【解析】本试题主要是考查了三角函数的化简和变形,以及运用三角函数的性质求解最值问题的综合运用试题。
查看习题详情和答案>>
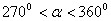 ,三角函数式
,三角函数式 的化简结果为( )
的化简结果为( )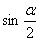 B.
B.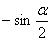 C.
C.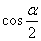 D.
D.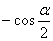
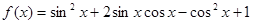
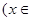 R
R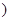 .
.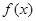 的最大值,并指出此时
的最大值,并指出此时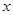 的值.
的值.
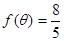 ,求
,求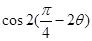 的值.
的值.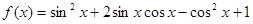 =
=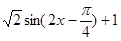 ,然后利用
,然后利用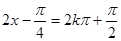 是,函数取得最大值
是,函数取得最大值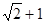 (2)中,结合(1)中的结论,然后由
(2)中,结合(1)中的结论,然后由
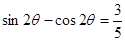 ,两边平方得
,两边平方得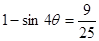 即
即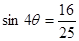 ,因此
,因此