摘要:点与曲线的关系 若曲线C的方程是f(x,y)=0.则点P0(x0,y0)在曲线C上f(x0,y0)=0, 点P0(x0,y0)不在曲线C上f(x0,y0)≠0两条曲线的交点 若曲线C1.C2的方程分别为f1(x,y)=0,f2(x,y)=0,则点P0(x0,y0)是C1.C2的交点 方程组有n个不同的实数解.两条曲线就有n个不同的交点,方程组没有实数解.曲线就没有交点.
网址:http://m.1010jiajiao.com/timu_id_4019974[举报]
在极坐标系中,直线l的方程为![]() ,在直角坐标系xOy中,圆C的参数方程为
,在直角坐标系xOy中,圆C的参数方程为![]() .
.
(Ⅰ)判断直线l与圆C的位置关系;
(Ⅱ)设点Q(x,y)是曲线C上的一个动点,若不等式![]() 有解,求m的取值范围.
有解,求m的取值范围.
平面内与两定点![]() 连线的斜率之积等于非零常数m的点的轨迹,加
连线的斜率之积等于非零常数m的点的轨迹,加
上A1、A2两点所在所面的曲线C可以是圆、椭圆或双曲线.
(Ⅰ)求曲线C的方程,并讨论C的形状与m的位置关系;
(Ⅱ)当m=-1时,对应的曲线为C1:对给定的![]() ,对应的曲线为C2,
,对应的曲线为C2,
设F1、F2是C2的两个焦点,试问:在C1上,是![]() 否存在点N,使得△F1NF2的面
否存在点N,使得△F1NF2的面
积![]() ,若存在,求
,若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知圆![]() 轴于A,B两点,曲线C是以AB为长轴,离心率为
轴于A,B两点,曲线C是以AB为长轴,离心率为![]() 的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点作直线PF的垂线交直线
的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点作直线PF的垂线交直线![]() 于点Q.
于点Q.
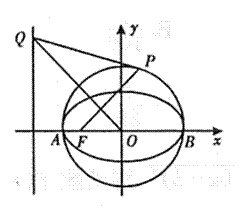 (1)求椭圆C的标准方程;w.w.w.k.s.5.u.c.o.m
(1)求椭圆C的标准方程;w.w.w.k.s.5.u.c.o.m ![]()
(2)若点P的坐标为(1,1),求证:直线PQ圆O相切;
(3)试探究:当点P在圆O上运动时(不与A、B重合),直线PQ与圆O是否保持相切的位置关系?若是,请证明;若不是,请说明理由(一、二、五中必做,其它学校选做)。.
查看习题详情和答案>>
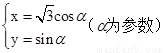 .
.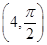 ,判断点P与直线l的位置关系;
,判断点P与直线l的位置关系;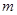 ,
,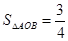 ;
;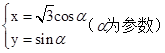 .
.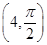 ,判断点P与直线l的位置关系;
,判断点P与直线l的位置关系;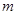 ,
,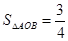 ;
;