摘要：分析法与综合法是对立统一的两个方面.前者执果索因.利于思考.因为它方向明确.思路自然.易于掌握,后者是由因导果.宜于表述.因为它条理清晰.形式简洁.适合人们的思维习惯.但是.用分析法探求证明不等式.只是一种重要的探求方式.而不是一种好的书写形式.因为它叙述较繁.如果把“只需证明 等字眼不写.就成了错误.而用综合法书写的形式.它掩盖了分析.探索的过程.因而证明不等式时.分析法.综合法常常是不能分离的.如果使用综合法证明不等式.难以入手时常用分析法探索证题的途径.之后用综合法形式写出它的证明过程.以适应人们习惯的思维规律.还有的不等式证明难度较大.需一边分析.一边综合.实现两头往中间靠以达到证题的目的.这充分表明分析与综合之间互为前提.互相渗透.互相转化的辩证统一关系.分析的终点是综合的起点.综合的终点又成为进一步分析的起点.
网址：http://m.1010jiajiao.com/timu_id_4019762[举报]
若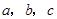
是不全相等的实数，求证：
．
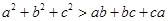证明过程如下：
，
，
，
，
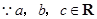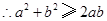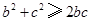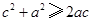又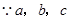
不全相等，
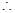以上三式至少有一个“
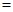”不成立，
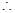将以上三式相加得
，
．
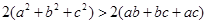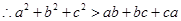此证法是（ ）
A．分析法 B．综合法 C．分析法与综合法并用 D．反证法
查看习题详情和答案>>
若a，b，c是不全相等的实数，求证：a2＋b2＋c2>ab＋bc＋ca.
证明过程如下：
∵a、b、c∈R，∴a2＋b2≥2ab，
b2＋c2≥2bc，c2＋a2≥2ac，
又∵a，b，c不全相等，
∴以上三式至少有一个“＝”不成立，
∴将以上三式相加得2(a2＋b2＋c2)>2(ab＋bc＋ac)，
∴a2＋b2＋c2>ab＋bc
＋ca.
此证法是( )
(A)分析法 (B)综合法
(C)分析法与综合法并用 (D)反证法
查看习题详情和答案>>
－1＞
－
．证明：要证
－1＞
－
，只需证
＋
＞
＋1，即证7＋2
＋5＞11＋2
＋1，
＞
，因为35＞11，所以原不等式成立．以上证明运用了