摘要：17．竖直放置的轻弹簧的劲度系数为,下端固定在地面上.上端与轻质平板相连.平板与地面间的距离为.如图5所示.现将一物块.轻轻地放在平板中心.让它从静止开始往下运动.直至物块速度为零.此时平板与地面间的距离为.则此时弹簧的弹性势能Ep= .
网址：http://m.1010jiajiao.com/timu_id_4018325[举报]
竖直放置的轻弹簧的劲度系数为k，下端固定在地面上，上端与轻质平板相连，平板与地面间的距离为h1，如图所示，现将一物块，轻轻地放在平板中心，让它从静止开始往下运动，直至物块速度为零，此时平板与地面间的距离为h2，则此时弹簧的弹性势能Ep=mg（h1-h2）
mg（h1-h2）
．轻质弹簧的劲度系数为k，下端固定一个质量为m的金属球，上端悬挂在天花板上，处于静止状态。沿竖直方向向下拉小球，使其发生一段位移，然后释放，小球将沿竖直方向上下振动。若弹簧的形变总在弹性限度以内。用x表示小球相对于平衡位置的位移，不计空气阻力，求振子回复力F的表达式和小球加速度的表达式。
查看习题详情和答案>>
轻质弹簧的劲度系数为k，下端固定一个质量为m的金属球，上端悬挂在天花板上，处于静止状态。沿竖直方向向下拉小球，使其发生一段位移，然后释放，小球将沿竖直方向上下振动。若弹簧的形变总在弹性限度以内。用x表示小球相对于平衡位置的位移，不计空气阻力，求振子回复力F的表达式和小球加速度的表达式。
查看习题详情和答案>>
劲度系数为k的轻弹簧，竖直放置在地面上，其上端固定有质量为M的钢板，处于静止状态，如图，现有一质量为m的小球从距钢板H的高处自由下落并与之发生碰撞，碰撞中无机械能损失．已知M=3m，弹簧振子的周期T=2π
|
（1）小球与钢板第一次碰撞后，小球的速度v1及钢板的速度v2的大小和方向；
（2）要使小球与钢板每次都在同一高度相碰（即钢板的初始位置），求钢板质量的最大值．
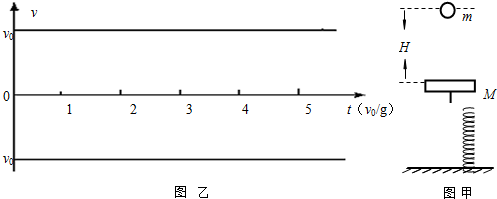
劲度系数为k的轻弹簧，竖直放置在地面上，其上端固定有质量为M的钢板，处于静止状态，如图甲所示，现有一质量为m的小球从距钢板H的高处自由下落并与之发生碰撞，碰撞时间极短且无机械能损失．已知M=3m，弹簧振子的周期T=2π
．
（1）求小球与钢板第一次碰撞后瞬间，小球的速度v1和钢板的速度v2．
（2）要使小球与钢板每次都在同一高度相碰（即钢板的初始位置），求钢板质量的最大值．
（3）以小球自由下落的瞬间为计时起点，以向下为正方向，以
的值作为1个时间单位（v0为小球第一次刚落到钢板时的速度值）．试在图乙中画出小球的v-t图线；要求至少画出小球与钢板发生第三次碰撞前的图线）．
查看习题详情和答案>>
| M/k |
（1）求小球与钢板第一次碰撞后瞬间，小球的速度v1和钢板的速度v2．
（2）要使小球与钢板每次都在同一高度相碰（即钢板的初始位置），求钢板质量的最大值．
（3）以小球自由下落的瞬间为计时起点，以向下为正方向，以
| v0 |
| g |