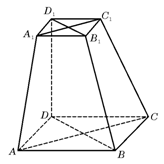
摘要： 如图.四棱锥F-ABCD的底面ABCD是菱形.其对角线AC=2.BD=.AE.CF都与平面ABCD垂直.AE=1.CF=2. (I)求二面角B-AF-D的大小, (II)求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积. 本小题主要考查直线与直线.直线与平面.平面与平面的位置关系.相交平面所成二面角以及空间几何体的体积计算等知识.考查空间想象能力和推理论证能力.利用综合法或向量法解决立体几何问题的能力.本小题满分13分. 解:连接AC.BD交于菱形的中心O.过O作OGAF. G为垂足.连接BG.DG.由BDAC.BDCF得BD平面ACF.故BDAF. 于是AF平面BGD.所以BGAF.DGAF.BGD为二面角B-AF-D 的平面角. 由. .得. 由.得 以A为坐标原点...方向分别为x轴.y轴.z轴的正方向建立空间直角坐标系 设平面ABF的法向量.则由得 令.得. 同理.可求得平面ADF的法向量. 由知.平面ABF与平面ADF垂直.二面角B-AF-D的大小等于. (II)连EB.EC.ED.设直线AF与直线CE相交于点H.则四棱锥E-ABCD与四棱锥F-ABCD的公共部分为四棱锥H-ABCD.过H作HP⊥平面ABCD.P为垂足. 因为EA⊥平面ABCD.FC⊥平面ABCD..所以平面ACFE⊥平面ABCD.从而 由得. 又因为 故四棱锥H-ABCD的体积
网址：http://m.1010jiajiao.com/timu_id_4017295[举报]
18(本小题满分12分)
下表提供了某厂节能降耗技术改进后生产甲产品过程中记录的产量x(吨)与相应的
生产能耗y(吨标准煤)的几组对照数据。
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程y=
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤，试根据（2）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？
（参考数值：3×2.5+4×3+5×4+6×4.5=66.5）
查看习题详情和答案>>
中，内角A、b、c的对边长分别为a、b、c.已知
，且
，求b.18(本小题满分12分)
下表提供了某厂节能降耗技术改进后生产甲产品过程中记录的产量x(吨)与相应的
生产能耗y(吨标准煤)的几组对照数据。
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程y=
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤，试根据（2）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？
（参考数值：3×2.5+4×3+5×4+6×4.5=66.5）
查看习题详情和答案>>
中,四边形ABCD是边 
是边长为1的正方
平面
与
共面，
与
共面．
的大小(用反三角函数值表示).
，若他命中目标的概率与距离的平方成反比，且各次射击都是独立的。