摘要：1?如图所示.已知面..二面角的平面角为. 求证: 证明:过作的垂线.垂足为.连接 ∵平面.平面. ∴ ∴为二面角的平面角. 即 ∵面 ∴ ∵是直角三角形 ∴ 又∵ ∴ ∴即 说明:这是推广的射影定理.也是求二面角平面角的一种方法2．如图.在空间四边形中.是正三角形.是等腰直角三角形.且.又二面角为直二面角.求二面角的大小 解:过作于 ∵二面角为直二面角 ∴面 取中点.为中点.连接 ∵ ∴ ∴ ∴ ∴为二面角的平面角 令.则 ∴ ∴在中 ∴ 即二面角的大小为
网址：http://m.1010jiajiao.com/timu_id_4015576[举报]
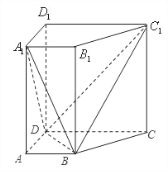如图所示，已知直四棱柱ABCD-A1B1C1D1中，AD⊥DCAB∥DC，且满足DC-DD1=2AD=2AB=2．
（1）求证：DB⊥平面B1BCC；
（2）求二面角A1-BD-C1的余弦值． 查看习题详情和答案>>
如图所示
，已知在矩形ABCD中，AB=1，BC=a（a＞0），PA⊥平面ABCD，且PA=1．
（I）问当实数a在什么范围时，BC边上能存在点Q，使得PQ⊥QD？
（II）当BC边上有且仅有一个点Q使得PQ⊥OD时，求二面角Q-PD-A的余弦值大小． 查看习题详情和答案>>
，已知在矩形ABCD中，AB=1，BC=a（a＞0），PA⊥平面ABCD，且PA=1．（I）问当实数a在什么范围时，BC边上能存在点Q，使得PQ⊥QD？
（II）当BC边上有且仅有一个点Q使得PQ⊥OD时，求二面角Q-PD-A的余弦值大小． 查看习题详情和答案>>
如图所示，已知多面体P-ABCD的直观图（图1）和它的三视图（图2），
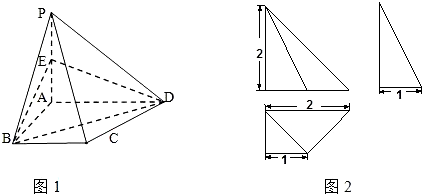
（Ⅰ）在棱PA上是否存在点E，使得PC∥平面EBD？若存在，求PE：PA的值，并证明你的结论；若不存在，说明理由；
（Ⅱ）求二面角B-PC-D的大小．（若不是特殊角请用反三角函数表示） 查看习题详情和答案>>
（Ⅰ）在棱PA上是否存在点E，使得PC∥平面EBD？若存在，求PE：PA的值，并证明你的结论；若不存在，说明理由；
（Ⅱ）求二面角B-PC-D的大小．（若不是特殊角请用反三角函数表示） 查看习题详情和答案>>
如图所示，已知矩形ABCD中，AB=