摘要:例1 求函数的最大值.下列解法是否正确?为什么? 解一: .∴ 解二:当即时. 答:以上两种解法均有错误 解一错在取不到“= .即不存在使得, 解二错在不是定值 正确的解法是: 当且仅当即时 例2 若.求的最值 解: ∵ ∴ 从而 即 例3设且.求的最大值 解:∵ ∴ 又.∴ 即 例4 已知且.求的最小值 解: 当且仅当即时 例5 将一块边长为的正方形铁皮.剪去四个角.作成一个无盖的铁盒.要使其容积最大.剪去的小正方形的边长为多少?最大容积是多少? 解:设剪去的小正方形的边长为则其容积为 当且仅当即时取“= 即当剪去的小正方形的边长为时.铁盒的容积为 例6 已知0 < x < 1, 0 < a < 1.试比较的大小 解一: ∵0 < 1 - x2 < 1, ∴ ∴ 解二: ∵0 < 1 - x2 < 1, 1 + x > 1, ∴ ∴ ∴ 解三:∵0< x <1.∴0 < 1 - x < 1, 1< 1 + x < 2, ∴ ∴左 - 右 = ∵0< 1 - x2 <1, 且0< a <1 ∴ ∴ 例7 已知x2 = a2 + b2.y2 = c2 + d2.且所有字母均为正.求证:xy≥ac + bd 证一:∵a, b, c, d, x, y都是正数 ∴要证:xy≥ac + bd 只需证:(xy)2≥(ac + bd)2 即 (a2 + b2)(c2 + d2)≥a2c2 + b2d2 + 2abcd 展开得:a2c2 + b2d2 + a2d2 + b2c2≥a2c2 + b2d2 + 2abcd 即 a2d2 + b2c2≥2abcd 由基本不等式.显然成立,∴xy≥ac + bd 证二:xy = ≥ 证三:∵x2 = a2 + b2.∴不妨设a = xsina, b = xcosa ∵y2 = c2 + d2 ∴不妨设 c = ysinb, d = ycosb ∴ac + bd = xysinasinb + xycosacosb = xycos≤xy 例8 已知x1, x2均为正数.求证: 证一:由于不等式两边均为正数.平方后只须证: 即 再平方 化简整理得 ∴原式成立 证二:假设 化简可得 ∴原式成立 证三:构造矩形ABCD.使AB = CD = 1, BP = x1, PC = x2 当ÐAPB = ÐDPC时.AP + PD为最短取BC中点M.有ÐAMB = ÐDMC, BM = MC =,∴ AP + PD ≥ AM + MD 即 ∴
网址:http://m.1010jiajiao.com/timu_id_4015543[举报]
(本题满分18分)
对于定义域为D的函数,如果存在区间,同时满足:
①在内是单调函数;
②当定义域是时,的值域也是.
则称是该函数的“和谐区间”.
(1)求证:函数不存在“和谐区间”.
(2)已知:函数()有“和谐区间”,当变化时,求出的最大值.
(3)易知,函数是以任一区间为它的“和谐区间”.试再举一例有“和谐区间”的函数,并写出它的一个“和谐区间”.(不需证明,但不能用本题已讨论过的及形如的函数为例)
查看习题详情和答案>>
对于定义域为D的函数y=f(x),如果存在区间[m,n]⊆D,同时满足:
①f(x)在[m,n]内是单调函数;
②当定义域是[m,n]时,f(x)的值域也是[m,n].则称[m,n]是该函数的“和谐区间”.
(1)求证:函数y=g(x)=3-
不存在“和谐区间”.
(2)已知:函数y=
(a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n-m的最大值.
(3)易知,函数y=x是以任一区间[m,n]为它的“和谐区间”.试再举一例有“和谐区间”的函数,并写出它的一个“和谐区间”.(不需证明,但不能用本题已讨论过的y=x及形如y=
的函数为例)
查看习题详情和答案>>
①f(x)在[m,n]内是单调函数;
②当定义域是[m,n]时,f(x)的值域也是[m,n].则称[m,n]是该函数的“和谐区间”.
(1)求证:函数y=g(x)=3-
| 5 |
| x |
(2)已知:函数y=
| (a2+a)x-1 |
| a2x |
(3)易知,函数y=x是以任一区间[m,n]为它的“和谐区间”.试再举一例有“和谐区间”的函数,并写出它的一个“和谐区间”.(不需证明,但不能用本题已讨论过的y=x及形如y=
| bx+c |
| ax |
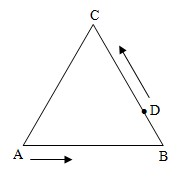 例2:如图:△ABC是边长为3厘米的正三角形,D是BC边上靠近点B的三等分点,甲、乙两个质点分别从点A、D同时出发,都以1厘米/秒的速度按图示方向沿三角形的边作匀速运动,经过时间t(0≤t≤3)秒后,两质点的距离为S(t).
例2:如图:△ABC是边长为3厘米的正三角形,D是BC边上靠近点B的三等分点,甲、乙两个质点分别从点A、D同时出发,都以1厘米/秒的速度按图示方向沿三角形的边作匀速运动,经过时间t(0≤t≤3)秒后,两质点的距离为S(t).(1)写出函数S(t)
(2)求S(t)的最大值和最小值,并求取得最大值、最小值时相应的t的值.
 不存在“和谐区间”.
不存在“和谐区间”. (a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n-m的最大值.
(a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n-m的最大值. 的函数为例)
的函数为例)