摘要：22．已知:直线交椭圆于.两点.且(为坐标原点) (1)求证:椭圆过定点, (2)若椭圆的离心率在上变化时.求椭圆长轴的取值范围. 福建省福州八县(市)一中09-10学年高二上学期期末联考
网址：http://m.1010jiajiao.com/timu_id_4014747[举报]
(本题满分14分)
已知椭圆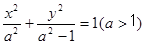
的左右焦点为
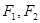，抛物线C：
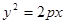以F2为焦点且与椭圆相交于点M，直线F1M与抛物线C相切。
（Ⅰ）求抛物线C的方程和点M的坐标；
（Ⅱ）过F2作抛物线C的两条互相垂直的弦AB、DE，设弦AB、DE的中点分别为F、N，求证直线FN恒过定点；
查看习题详情和答案>>
(本题满分14分)
已知椭圆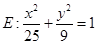
，直线
，F为椭圆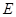
的右焦点，M为椭圆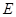上任意一点，记M到直线L的距离为d.
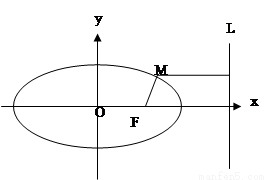
(Ⅰ) 求证：
为定值；
(Ⅱ) 设过右焦点F的直线m的倾斜角为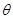
，m交椭圆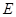于A、B两点，且
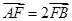，求
的值。
查看习题详情和答案>>
(本题满分14分)
已知椭圆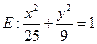
，直线
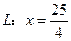，F为椭圆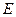
的右焦点，M为椭圆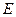上任意一点，记M到直线L的距离为d.
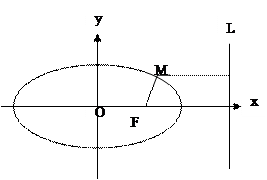
(Ⅰ) 求证：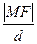
为定值；
(Ⅱ) 设过右焦点F的直线m的倾斜角为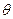
，m交椭圆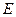于A、B两点，且
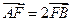，求
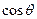的值。
已知椭圆
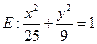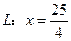，直线，F为椭圆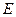的右焦点，M为椭圆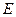上任意一点，记M到直线L的距离为d.(Ⅰ) 求证：
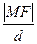为定值；(Ⅱ) 设过右焦点F的直线m的倾斜角为
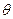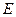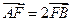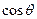，m交椭圆于A、B两点，且，求的值。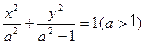
的左右焦点为
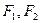，抛物线C：
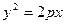以F2为焦点且与椭圆相交于点M，直线F1M与抛物线C相切。
的两个焦点为F1、F2，短轴两端点B1、B2，已知
）、Q的直线对称？若能，求出k的取值范围；若不能，请说明理由．