摘要：二次函数: ①.若二次函数(或)在R上恒成立.则有(或), ②.若二次函数(或)在指定区间上恒成立.可以利用韦达定理以及根的分布等知识求解. 例1．已知函数.若对于任一实数.与的值至少有一个为正数.则实数的取值范围是( ) A． C．分析:与的函数类型.直接受参数的影响.所以首先要对参数进行分类讨论.然后转换成不等式的恒成立的问题利用函数性质及图像解题. 解析:当时.在上恒成立.而在上恒成立.显然不满足题意, 当时.在上递减且只在上恒成立. 而是一个开口向下且恒过定点(0.1)的二次函数.显然不满足题意. 当时.在上递增且在上恒成立. 而是一个开口向上且恒过定点(0.1)的二次函数.要使对任一实数. 与的值至少有一个为正数则只需在上恒成立. 则有或解得或. 综上可得即. 故选B. 例2设函数． (1)对于任意实数.恒成立.求的最大值. 解析:(1) , 对,, 即在上恒成立, , 得.即的最大值为.

网址：http://m.1010jiajiao.com/timu_id_4014514[举报]

已知二次函数f（x）=x²+x的定义域D 恰是不等式 f（-x）+f（x）≤2|x|的解集，其值域为A．函数 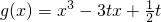$数学公式$ 的定义域为[0，1]，值域为B．
（1）求f （x）的定义域D和值域 A；
（2）（理）试用函数单调性的定义解决下列问题：若存在实数x₀∈（0，1），使得函数 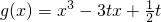$数学公式$ 在[0，x₀]上单调递减，在[x₀，1]上单调递增，求实数t的取值范围并用t表示x₀．
（3）（理）是否存在实数t，使得A⊆B成立？若存在，求实数t 的取值范围；若不存在，请说明理由．
（4）（文）是否存在负实数t，使得A⊆B成立？若存在，求负实数t 的取值范围；若不存在，请说明理由．
（5）（文）若函数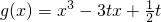 $数学公式$ 在定义域[0，1]上单调递减，求实数t的取值范围．

查看习题详情和答案>>

已知二次函数满足以下两个条件：

①不等式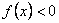的解集是（-2，0） ②函数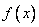在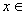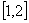上的最小值是3

（Ⅰ）求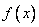的解析式；

（Ⅱ）若点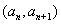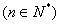在函数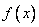的图象上，且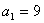

（ⅰ）求证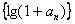：数列为等比数列

（ⅱ）令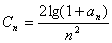，是否存在整数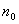使得数列取到最小值？若有，请求出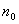的值；没有，请说明理由。

查看习题详情和答案>>

已知二次函数f（x）=ax²+bx，f（x+1）为偶函数，函数f（x）的图象与直线y=x相切．
（I）求f（x）的解析式；
（II）已知k的取值范围为[

，+∞），则是否存在区间[m，n]（m＜n），使得f（x）在区间[m，n]上的值域恰好为[km，kn]？若存在，请求出区间[m，n]；若不存在，请说明理由．

查看习题详情和答案>>

对于二次函数f（x）=ax²+bx+c，有下列命题：
①若f（p）=f（q）（p≠q），则f（p+q）=c；
②若f（p）=q，f（q）=p，（p≠q），则f（p+q）=-（p+q）；
③若f（p+q）=c（p≠q），则p+q=0或f（p）=f（q）．
其中一定正确的命题是

．（写出所有正确命题的序号）

查看习题详情和答案>>

已知二次函数f（x）=ax²+bx+c（a≠0）
（1）若f（-1）=0，试判断函数f（x）零点的个数；
（2）是否存在a，b，c∈R，使f（x）同时满足以下条件：①f（-1+x）=f（-1-x）且f（x）≥0；
②对0≤f（x）-x≤

（x-1）²．若存在，求出a，b，c的值；若不存在，请说明理由．

查看习题详情和答案>>