摘要：等比数列的性质: (1)当时.则有.特别地.当时.则有.如(1)在等比数列中..公比q是整数.则= 各项均为正数的等比数列中.若.则 . (2) 若是等比数列.则..成等比数列,若成等比数列.则.成等比数列, 若是等比数列.且公比.则数列 .-也是等比数列.当.且为偶数时.数列 .-是常数数列0.它不是等比数列. 如(1)已知且.设数列满足.且.则 . (答:),(2)在等比数列中.为其前n项和.若.则的值为 (3)若.则为递增数列,若, 则为递减数列,若 .则为递减数列,若, 则为递增数列,若.则为摆动数列,若.则为常数列. (4) 当时..这里.但.这是等比数列前项和公式的一个特征.据此很容易根据.判断数列是否为等比数列.如若是等比数列.且.则＝ (5) .如设等比数列的公比为.前项和为.若成等差数列.则的值为 (6) 在等比数列中.当项数为偶数时.,项数为奇数时.. (7)如果数列既成等差数列又成等比数列.那么数列是非零常数数列.故常数数列仅是此数列既成等差数列又成等比数列的必要非充分条件.如设数列的前项和为(). 关于数列有下列三个命题:①若.则既是等差数列又是等比数列,②若.则是等差数列,③若.则是等比数列.这些命题中.真命题的序号是
网址：http://m.1010jiajiao.com/timu_id_4014010[举报]
等差数列和等比数列具有一些相似的性质，由等差数列的下列性质类比等比数列的性质：
等差数列的性质 | 等比数列的性质 |
若m+n=p+q,则am+an=ap+aq | ① |
若m+n=2p,则am+an=2ap | ② |
am=an+(m-n)d,d= | ③ |
ak,a(k+m),a(k+2m),…构成公差为md的等差数列 | ④ |
Sn是等差数列{an}的前n项和，则Sn，S2n-Sn，S3n-S2n构成公差为n2d的等差数列 | ⑤ |
已知数列
是首项为
的等比数列，且满足
.
（1） 求常数
的值和数列的通项公式；
（2） 若抽去数列中的第一项、第四项、第七项、……、第
项、……，余下的项按原来的顺序组成一个新的数列
，试写出数列的通项公式；
（3） 在（2）的条件下，设数列的前
项和为
.是否存在正整数，使得
？若存在，试求所有满足条件的正整数的值；若不存在，请说明理由.
【解析】第一问中解：由
得
，，
又因为存在常数p使得数列
为等比数列，
则
即
，所以p=1
故数列为首项是2，公比为2的等比数列，即
.
此时
也满足，则所求常数的值为1且
第二问中，解：由等比数列的性质得：
（i）当
时，
；
（ii） 当
时，
，
所以
第三问假设存在正整数n满足条件，则
，
则（i）当时，
，
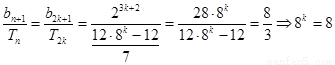
查看习题详情和答案>>
已知等差数列{an}，公差为d,前n项和为Sn，有如下性质：
（1）通项an=am+(n-m)d.
(2)若m+n=p+q,其中m、n、p、q∈N+,则am+an=ap+aq.
(3)若m+n=2p,m、n、p∈N+，则am+an=2ap.
(4)Sn,S2n-Sn,S3n-S2n构成等差数列.
类比得出等比数列的性质.
查看习题详情和答案>>