摘要:4.对较复杂的不等式先用分析法探求证明途径.再用综合法,或比较法加以证明.
网址:http://m.1010jiajiao.com/timu_id_4013900[举报]
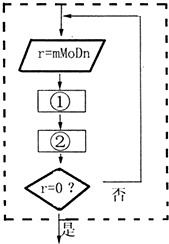 辗转相除法的基本步骤是用较大的数(用变量m表示)除以较小的数(用变量n表示)
辗转相除法的基本步骤是用较大的数(用变量m表示)除以较小的数(用变量n表示)除式为m=n•q+r(0≤r<n),这是一个反复执行的循环过程,如图个循环结构的程序框图,则①、②两处应依次填写
m=n
m=n
、n=r
n=r
.自然状态下的鱼类是一种可再生的资源,为了持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响.用xn表示某鱼群在第n年初的总量,n∈N*,且x1>0.不考虑其他因素,设在第n年内鱼群的繁殖量及被捕捞量都与xn成正比,死亡量与xn2成正比,这些比例系数依次为正数a,b,c其中b称为捕捞强度.
(1)求xn+1与xn的关系式;
(2)设a=2,c=1,为了保证对任意x1∈(0,2),都有xn>0,n∈N*,则捕捞强度B的最大允许值是多少?证明你的结论.
查看习题详情和答案>>
(1)求xn+1与xn的关系式;
(2)设a=2,c=1,为了保证对任意x1∈(0,2),都有xn>0,n∈N*,则捕捞强度B的最大允许值是多少?证明你的结论.
自然状态下的鱼类是一种可再生资源,为持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响.用xn表示某鱼群在第n年年初的总量,n∈N*,且x1>0.不考虑其它因素,设在第n年内鱼群的繁殖量及捕捞量都与xn成正比,死亡量与xn2成正比,这些比例系数依次为正常数a,b,c.
(Ⅰ)求xn+1与xn的关系式;
(Ⅱ)猜测:当且仅当x1,a,b,c满足什么条件时,每年年初鱼群的总量保持不变?(不要求证明)
(Ⅲ)设a=2,b=1,为保证对任意x1∈(0,2),都有xn>0,n∈N*,则捕捞强度b的
最大允许值是多少?证明你的结论. 查看习题详情和答案>>
(Ⅰ)求xn+1与xn的关系式;
(Ⅱ)猜测:当且仅当x1,a,b,c满足什么条件时,每年年初鱼群的总量保持不变?(不要求证明)
(Ⅲ)设a=2,b=1,为保证对任意x1∈(0,2),都有xn>0,n∈N*,则捕捞强度b的
最大允许值是多少?证明你的结论. 查看习题详情和答案>>
 表示某鱼群在第
表示某鱼群在第 年初的总量,
年初的总量, ,且
,且 。不考虑其他因素,设在第
。不考虑其他因素,设在第 成正比,这些比例系数依次为正数
成正比,这些比例系数依次为正数 其中
其中 称为捕捞强度。
称为捕捞强度。 与
与 ,为了保证对任意
,为了保证对任意 ,都有
,都有 ,则捕捞强度
,则捕捞强度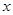 的不等式
的不等式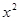 +25+|
+25+|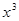 -5
-5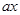 在[1,12]上恒成立,求实数
在[1,12]上恒成立,求实数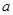 的取值范围”提出各自的解题思路.
的取值范围”提出各自的解题思路.