摘要： 空间直线. (1)空间直线位置分三种:相交.平行.异面. 相交直线-共面有且有一个公共点,平行直线-共面没有公共点,异面直线-不同在任一平面内. (2)异面直线判定定理:过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.(不在任何一个平面内的两条直线) (3)平行公理:平行于同一条直线的两条直线互相平行. (4)等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同.那么这两个角相等 推论:如果两条相交直线和另两条相交直线分别平行.那么这两组直线所成锐角相等.
网址：http://m.1010jiajiao.com/timu_id_4008896[举报]
6、在平面上，两条直线的位置关系有相交、平行、重合三种．已知α，β是两个相交平面，空间两条直线l1，l2在α上的射影是直线S1，S2，l1，l2在β上的射影是直线t1，t2．用S1与S2，t1与t2的位置关系，写出一个总能确定l1与l2是异面直线的充分条件：
查看习题详情和答案>>
S1∥S2，并且t1与t2相交（或：t1∥t2，并且S1与S2相交）
．
10.在平面上，两条直线的位置关系有相交、平行、重合三种. 已知
是两个相交平面，空间两条直线l1、l2在
上的射影是直线s1、s2，l1、l2在
上的射影是直线t1、t2.用
与
，
与
的位置关系，写出一个总能确定
与
是异面直线的充分条件： .
查看习题详情和答案>>
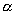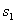是两个相交平面，空间两条直线l1、l2在上的射影是直线s1、s2，l1、l2在上的射影是直线t1、t2.用与，与的位置关系，写出一个总能确定与是异面直线的充分条件： .
查看习题详情和答案>>
在平面上，两条直线的位置关系有相交、平行、重合三种．已知α，β是两个相交平面，空间两条直线l1，l2在α上的射影是直线S1，S2，l1，l2在β上的射影是直线t1，t2．用S1与S2，t1与t2的位置关系，写出一个总能确定l1与l2是异面直线的充分条件： ．
查看习题详情和答案>>
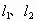在α上的射影是直线
，
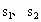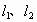在β上的射影是直线
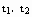．用
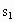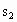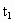与
，
与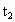
的位置关系，写出一个总能确定
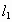与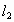
是异面直线的充分条件：_____________．