摘要:4.注意深刻理解等差数列与等比数列的定义及其等价形式,
网址:http://m.1010jiajiao.com/timu_id_4008873[举报]
(考生注意:本题请从以下甲乙两题中任选一题作答,若两题都答只以甲题计分)
甲:设数列{bn}的前n项和为Sn,且bn=2-Sn;数列{an} 为等差数列,且a5=9,a7=13.
(Ⅰ)求数列 {bn} 的通项公式;
(Ⅱ)若cn=anbn(n=1,2,3,…),Tn为数列{cn}的前n项和,求Tn.
乙:定义在[-1,1]上的奇函数f(x),已知当x∈[-1,0]时,f(x)=
-
(a∈R)
(Ⅰ)求f(x)在[0,1]上的最大值;
(Ⅱ)若f(x)是[0,1]上的增函数,求实数a的取值范围.
查看习题详情和答案>>
甲:设数列{bn}的前n项和为Sn,且bn=2-Sn;数列{an} 为等差数列,且a5=9,a7=13.
(Ⅰ)求数列 {bn} 的通项公式;
(Ⅱ)若cn=anbn(n=1,2,3,…),Tn为数列{cn}的前n项和,求Tn.
乙:定义在[-1,1]上的奇函数f(x),已知当x∈[-1,0]时,f(x)=
| 1 |
| 4x |
| a |
| 2x |
(Ⅰ)求f(x)在[0,1]上的最大值;
(Ⅱ)若f(x)是[0,1]上的增函数,求实数a的取值范围.
如图1:等边 可以看作由等边
可以看作由等边 绕顶点
绕顶点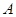 经过旋转相似变换得到.但是我们注意到图形中的
经过旋转相似变换得到.但是我们注意到图形中的 和
和 的关系,上述变换也可以理解为图形是由
的关系,上述变换也可以理解为图形是由 绕顶点
绕顶点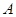 旋转
旋转 形成的.于是我们得到一个结论:如果两个正三角形存在着公共顶点,则该图形可以看成是由一个三角形绕着该顶点旋转
形成的.于是我们得到一个结论:如果两个正三角形存在着公共顶点,则该图形可以看成是由一个三角形绕着该顶点旋转 形成的.
形成的.

① 利用上述结论解决问题:如图2, 中,
中, 都是等边三角形,求四边形
都是等边三角形,求四边形 的面积;
的面积;
② 图3中,  ∽
∽ ,
, ,仿照上述结论,推广出符合图3的结论.(写出结论即可)
,仿照上述结论,推广出符合图3的结论.(写出结论即可)
查看习题详情和答案>>
 中,
中, ,点
,点 在直线y = x上,其中n = 1,2,3,….
在直线y = x上,其中n = 1,2,3,…. ,证明数列
,证明数列 是等比数列;
是等比数列;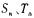 分别为数列
分别为数列 的前n项和,证明数列
的前n项和,证明数列 是等差数列
是等差数列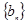 的前
的前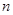 项和为
项和为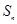 ,且
,且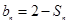 ;数列
;数列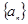 为等差数列,且
为等差数列,且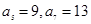
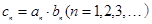 ,
, 为数列
为数列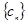 的前
的前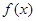 ,已知当
,已知当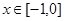 时,
时,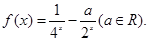
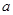 的取值范围
的取值范围