摘要:平面向量部分的复习应该注重向量的工具作用.紧紧围绕数形结合思想.扬长避短.解决问题,
网址:http://m.1010jiajiao.com/timu_id_4008834[举报]
将所有平面向量组成的集合记作R2,f是从R2到R2的映射,记作
=f(
)或(y1,y2)=f(x1,x2),其中x1,x2,y1,y2都是实数.定义映射f的模为:在|
|=1的条件下|
|的最大值,记做||f||.若存在非零向量
∈R2,及实数λ使得f(
)=λ
,则称λ为f的一个特征值.
(1)若f(x1,x2)=(
x1,x2),求||f||;
(2)如果f(x1,x2)=(x1+x2,x1-x2),计算f的特征值,并求相应的
;
(3)若f(x1,x2)=(a1x1+a2x2,b1x1+b2x2),要使f有唯一的特征值,实数a1,a2,b1,b2应满足什么条件?试找出一个映射f,满足以下两个条件:①有唯一的特征值λ,②||f||=|λ|,并验证f满足这两个条件.
查看习题详情和答案>>
| y |
| x |
| x |
| y |
| x |
| x |
| x |
(1)若f(x1,x2)=(
| 1 |
| 2 |
(2)如果f(x1,x2)=(x1+x2,x1-x2),计算f的特征值,并求相应的
| x |
(3)若f(x1,x2)=(a1x1+a2x2,b1x1+b2x2),要使f有唯一的特征值,实数a1,a2,b1,b2应满足什么条件?试找出一个映射f,满足以下两个条件:①有唯一的特征值λ,②||f||=|λ|,并验证f满足这两个条件.
将所有平面向量组成的集合记作R2,f是从R2到R2的映射,记作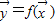 或(y1,y2)=f(x1,x2),其中x1,x2,y1,y2都是实数.定义映射f的模为:在|
或(y1,y2)=f(x1,x2),其中x1,x2,y1,y2都是实数.定义映射f的模为:在|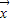 |=1的条件下|
|=1的条件下|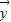 |的最大值,记做||f||.若存在非零向量
|的最大值,记做||f||.若存在非零向量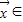 R2,及实数λ使得f(
R2,及实数λ使得f(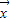 )=
)=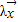 ,则称λ为f的一个特征值.
,则称λ为f的一个特征值.
(1)若f(x1,x2)=( x1,x2),求||f||;
x1,x2),求||f||;
(2)如果f(x1,x2)=(x1+x2,x1-x2),计算f的特征值,并求相应的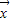 ;
;
(3)若f(x1,x2)=(a1x1+a2x2,b1x1+b2x2),要使f有唯一的特征值,实数a1,a2,b1,b2应满足什么条件?试找出一个映射f,满足以下两个条件:①有唯一的特征值λ,②||f||=|λ|,并验证f满足这两个条件.
查看习题详情和答案>>
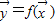 或(y1,y2)=f(x1,x2),其中x1,x2,y1,y2都是实数.定义映射f的模为:在|
或(y1,y2)=f(x1,x2),其中x1,x2,y1,y2都是实数.定义映射f的模为:在|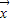 |=1的条件下|
|=1的条件下|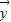 |的最大值,记做||f||.若存在非零向量
|的最大值,记做||f||.若存在非零向量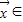 R2,及实数λ使得f(
R2,及实数λ使得f(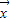 )=
)=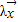 ,则称λ为f的一个特征值.
,则称λ为f的一个特征值.(1)若f(x1,x2)=(
 x1,x2),求||f||;
x1,x2),求||f||;(2)如果f(x1,x2)=(x1+x2,x1-x2),计算f的特征值,并求相应的
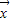 ;
;(3)若f(x1,x2)=(a1x1+a2x2,b1x1+b2x2),要使f有唯一的特征值,实数a1,a2,b1,b2应满足什么条件?试找出一个映射f,满足以下两个条件:①有唯一的特征值λ,②||f||=|λ|,并验证f满足这两个条件.
查看习题详情和答案>>
将所有平面向量组成的集合记作R2,f是从R2到R2的映射,记作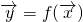 或(y1,y2)=f(x1,x2),其中x1,x2,y1,y2都是实数.定义映射f的模为:在|
或(y1,y2)=f(x1,x2),其中x1,x2,y1,y2都是实数.定义映射f的模为:在| |=1的条件下|
|=1的条件下| |的最大值,记做||f||.若存在非零向量
|的最大值,记做||f||.若存在非零向量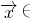 R2,及实数λ使得f(
R2,及实数λ使得f( )=
)=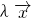 ,则称λ为f的一个特征值.
,则称λ为f的一个特征值.
(1)若f(x1,x2)=( x1,x2),求||f||;
x1,x2),求||f||;
(2)如果f(x1,x2)=(x1+x2,x1-x2),计算f的特征值,并求相应的 ;
;
(3)若f(x1,x2)=(a1x1+a2x2,b1x1+b2x2),要使f有唯一的特征值,实数a1,a2,b1,b2应满足什么条件?试找出一个映射f,满足以下两个条件:①有唯一的特征值λ,②||f||=|λ|,并验证f满足这两个条件.
查看习题详情和答案>>
将所有平面向量组成的集合记作R2,f是从R2到R2的映射,记作
=f(
)或(y1,y2)=f(x1,x2),其中x1,x2,y1,y2都是实数.定义映射f的模为:在|
|=1的条件下|
|的最大值,记做||f||.若存在非零向量
∈R2,及实数λ使得f(
)=λ
,则称λ为f的一个特征值.
(1)若f(x1,x2)=(
x1,x2),求||f||;
(2)如果f(x1,x2)=(x1+x2,x1-x2),计算f的特征值,并求相应的
;
(3)若f(x1,x2)=(a1x1+a2x2,b1x1+b2x2),要使f有唯一的特征值,实数a1,a2,b1,b2应满足什么条件?试找出一个映射f,满足以下两个条件:①有唯一的特征值λ,②||f||=|λ|,并验证f满足这两个条件.
查看习题详情和答案>>
| y |
| x |
| x |
| y |
| x |
| x |
| x |
(1)若f(x1,x2)=(
| 1 |
| 2 |
(2)如果f(x1,x2)=(x1+x2,x1-x2),计算f的特征值,并求相应的
| x |
(3)若f(x1,x2)=(a1x1+a2x2,b1x1+b2x2),要使f有唯一的特征值,实数a1,a2,b1,b2应满足什么条件?试找出一个映射f,满足以下两个条件:①有唯一的特征值λ,②||f||=|λ|,并验证f满足这两个条件.
将所有平面向量组成的集合记作R2,f是从R2到R2的映射,记作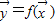 或(y1,y2)=f(x1,x2),其中x1,x2,y1,y2都是实数.定义映射f的模为:在|
或(y1,y2)=f(x1,x2),其中x1,x2,y1,y2都是实数.定义映射f的模为:在|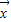 |=1的条件下|
|=1的条件下|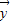 |的最大值,记做||f||.若存在非零向量
|的最大值,记做||f||.若存在非零向量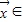 R2,及实数λ使得f(
R2,及实数λ使得f(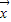 )=
)=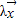 ,则称λ为f的一个特征值.
,则称λ为f的一个特征值.
(1)若f(x1,x2)=( x1,x2),求||f||;
x1,x2),求||f||;
(2)如果f(x1,x2)=(x1+x2,x1-x2),计算f的特征值,并求相应的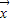 ;
;
(3)若f(x1,x2)=(a1x1+a2x2,b1x1+b2x2),要使f有唯一的特征值,实数a1,a2,b1,b2应满足什么条件?试找出一个映射f,满足以下两个条件:①有唯一的特征值λ,②||f||=|λ|,并验证f满足这两个条件.
查看习题详情和答案>>
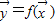 或(y1,y2)=f(x1,x2),其中x1,x2,y1,y2都是实数.定义映射f的模为:在|
或(y1,y2)=f(x1,x2),其中x1,x2,y1,y2都是实数.定义映射f的模为:在|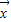 |=1的条件下|
|=1的条件下|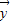 |的最大值,记做||f||.若存在非零向量
|的最大值,记做||f||.若存在非零向量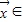 R2,及实数λ使得f(
R2,及实数λ使得f(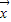 )=
)=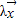 ,则称λ为f的一个特征值.
,则称λ为f的一个特征值.(1)若f(x1,x2)=(
 x1,x2),求||f||;
x1,x2),求||f||;(2)如果f(x1,x2)=(x1+x2,x1-x2),计算f的特征值,并求相应的
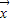 ;
;(3)若f(x1,x2)=(a1x1+a2x2,b1x1+b2x2),要使f有唯一的特征值,实数a1,a2,b1,b2应满足什么条件?试找出一个映射f,满足以下两个条件:①有唯一的特征值λ,②||f||=|λ|,并验证f满足这两个条件.
查看习题详情和答案>>