摘要：11．已知△ABC的边AB长为6.点C到A.B两点的距离之比为2∶1.则点C的轨迹方程为 ． 答案:(x-5)2+y2＝16(y≠0) 解析: 以AB所在直线为x轴.线段AB中点为原点.建立平面直角坐标系.则A.B(3,0)．设C(x.y). 由题意=2.
网址：http://m.1010jiajiao.com/timu_id_4007103[举报]
（2012•东莞二模）已知△ABC的边AB边所在直线的方程为x-3y-6=0，M（2，0）满足| BM |
| MC |
| AT |
| AB |
（1）求AC边所在直线的方程；
（2）求△ABC外接圆的方程；
（3）若动圆P过点N（-2，0），且与△ABC的外接圆外切，求动圆P的圆心的轨迹方程．
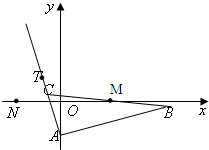已知△ABC的边AB边所在直线的方程为x-3y-6=0点B关于点M（2，0）的对称点为C，点T（-1，1）在AC边所在直线上且满足| AT |
| AB |
（I）求AC边所在直线的方程；
（II）求△ABC的外接圆的方程；
（III）若点N的坐标为（-n，0），其中n为正整数．试讨论在△ABC的外接圆上是否存在点P，使得|PN|=|PT|成立？说明理由． 查看习题详情和答案>>
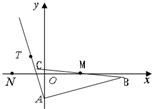已知△ABC的边AB所在直线的方程为x-3y-6=0，M（2，0）满足| BM |
| MC |
| AT |
| AB |
（1）求△ABC外接圆的方程；
（2）一动圆过点N（-2，0），且与△ABC的外接圆外切，求此动圆圆心的轨迹方程Γ；
（3）过点A斜率为k的直线与曲线Γ交于相异的P，Q两点，满足
| OP |
| OQ |
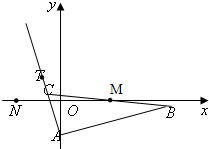已知△ABC的边AB边所在直线的方程为x-3y-6=0，M（2，0）满足
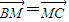，点T（-1，1）在AC边所在直线上且满足
．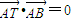