摘要:例13.求函数y=x+的最大.最小值 解:∵xR ∴可设x=sin(-) 则有y=sin +∣cos ∣ ∵- ∴cos≥0 ∴y=sin + cos=sin(+) ∵- ∴-≤≤+≤ ∴-1≤sin(+) 当=- 亦即x=-1 函数y=-1 当= 亦即x= 函数y= 上述例中都运用了三角代换能使某些代数函数的最值问题得到最解决.在这类题型的解题中.必需确定所设三角中角的变化范围.这是十分重要的环节.否则在后面的解题就得分类讨论或者发生矛盾的现象.甚至使整题前功尽弃.
网址:http://m.1010jiajiao.com/timu_id_4005978[举报]
函数y=Asin(ωx+φ),(A>0, ω>0, |φ|<
)的最小值是-2,在一个周期内图象最高点与最低点横坐标差是3π,又:图象过点(0,1),
求(1)函数解析式,并利用“五点法”画出函数的图象;
(2)函数的最大值、以及达到最大值时x的集合;
(3)该函数图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩得到?
(4)当x∈(0,
)时,函数的值域.
查看习题详情和答案>>
| π |
| 2 |
求(1)函数解析式,并利用“五点法”画出函数的图象;
(2)函数的最大值、以及达到最大值时x的集合;
(3)该函数图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩得到?
(4)当x∈(0,
| 3π |
| 2 |
我们将具有下列性质的所有函数组成集合M:函数y=f(x)(x∈D),对任意 均满足
均满足 ,当且仅当x=y时等号成立.
,当且仅当x=y时等号成立.
(1)若定义在(0,+∞)上的函数f(x)∈M,试比较f(3)+f(5)与2f(4)大小.
(2)给定两个函数: ,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.
,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.
(3)试利用(2)的结论解决下列问题:若实数m、n满足2m+2n=1,求m+n的最大值.
查看习题详情和答案>>
 均满足
均满足 ,当且仅当x=y时等号成立.
,当且仅当x=y时等号成立.(1)若定义在(0,+∞)上的函数f(x)∈M,试比较f(3)+f(5)与2f(4)大小.
(2)给定两个函数:
 ,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.
,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.(3)试利用(2)的结论解决下列问题:若实数m、n满足2m+2n=1,求m+n的最大值.
查看习题详情和答案>>
我们将具有下列性质的所有函数组成集合M:函数y=f(x)(x∈D),对任意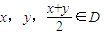 均满足
均满足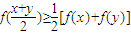 ,当且仅当x=y时等号成立.
,当且仅当x=y时等号成立.
(1)若定义在(0,+∞)上的函数f(x)∈M,试比较f(3)+f(5)与2f(4)大小.
(2)给定两个函数: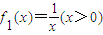 ,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.
,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.
(3)试利用(2)的结论解决下列问题:若实数m、n满足2m+2n=1,求m+n的最大值.
查看习题详情和答案>>
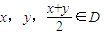 均满足
均满足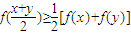 ,当且仅当x=y时等号成立.
,当且仅当x=y时等号成立.(1)若定义在(0,+∞)上的函数f(x)∈M,试比较f(3)+f(5)与2f(4)大小.
(2)给定两个函数:
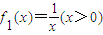 ,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.
,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.(3)试利用(2)的结论解决下列问题:若实数m、n满足2m+2n=1,求m+n的最大值.
查看习题详情和答案>>
我们将具有下列性质的所有函数组成集合M:函数y=f(x)(x∈D),对任意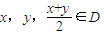 均满足
均满足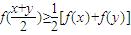 ,当且仅当x=y时等号成立.
,当且仅当x=y时等号成立.
(1)若定义在(0,+∞)上的函数f(x)∈M,试比较f(3)+f(5)与2f(4)大小.
(2)给定两个函数: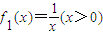 ,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.
,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.
(3)试利用(2)的结论解决下列问题:若实数m、n满足2m+2n=1,求m+n的最大值.
查看习题详情和答案>>
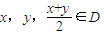 均满足
均满足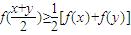 ,当且仅当x=y时等号成立.
,当且仅当x=y时等号成立.(1)若定义在(0,+∞)上的函数f(x)∈M,试比较f(3)+f(5)与2f(4)大小.
(2)给定两个函数:
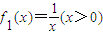 ,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.
,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.(3)试利用(2)的结论解决下列问题:若实数m、n满足2m+2n=1,求m+n的最大值.
查看习题详情和答案>>
| |||||||||||