摘要：例6．已知:定义在上的减函数.使得 对一切实数均成立.求实数的范围. 解:由题意可得 . 即 . 又 . . . . . 或 . 例7．如果∣x∣≤求函数f(x)=cos2x + sin x 的最大.最小值. 解:y= -- sin2x + sin x + 1 = --(sin x --)2 + 设 sin x = t 得y = --(t -- )2 + 由题设∣x∣≤. ∴ - ≤sin x ≤ ∴- ≤ t ≤ 因为f(x)在[-.]是增函数.在[.]是减函数 ∴当x = -时.= 当x = 时. = 上例就是利用在闭区间上求二次函数最值的方法.就可以求含三角式的二次函数的最值.但是在运用这个方法前.首先要将引用三角比之间的转换使式子中只含有同名的三角比.再把此三角比视为二次函数的自变量. 例8.在△ABC中.求cosAcosBcosC的最大值. 本题是一个经典习题.有多种解法.下面解法中把角C当作主元化为二次形式.再进行配方.又利用.此法具有一般性. 例9．设.求f (x)的最大.小值. 分析:二次函数.分类讨论 .令.所以 则ⅰ)当时.即:-4≤a≤4时.,当 -4≤a≤0时.,当 0≤a≤4时., ⅱ)当时.即a≤-4.,. ⅲ)当时.即a≥4.,.
网址：http://m.1010jiajiao.com/timu_id_4005976[举报]
已知函数
，
（1）当
时，求f（x）的反函数g（x）；
（2）求关于x的函数y=[g（x）]2-2ag（x）+3（a≤3）当x∈[-1.1]时的最小值h（a）；
（3）我们把同时满足下列两个性质的函数称为“和谐函数”：
①函数在整个定义域上是单调增函数或单调减函数；
②在函数的定义域内存在区间[p，q]（p＜q）使得函数在区间[p，q]上的值域为[p2，q2]．
（Ⅰ）判断（2）中h（x）是否为“和谐函数”？若是，求出p，q的值或关系式；若不是，请说明理由；
（Ⅱ）若关于x的函数y=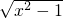
+t（x≥1）是“和谐函数”，求实数t的取值范围．
查看习题详情和答案>>
已知函数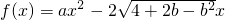
，
．
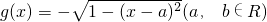（1）当b=0时，若f（x）在（-∞，2]上单调递减，求a的取值范围；
（2）求满足下列条件的所有整数对（a，b）：存在x0，使得f（x0）是f（x）的最大值，g（x0）是g（x）的最小值；
（3）对满足（II）中的条件的整数对（a，b），试构造一个定义在D=x|x∈R且x≠2k，k∈Z上的函数h（x），使h（x+2）=h（x），且当x∈（-2，0）时，h（x）=f（x）．
查看习题详情和答案>>
已知函数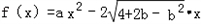
，
．
（1）当b=0时，若f（x）在（﹣∞，2]上单调递减，求a的取值范围；
（2）求满足下列条件的所有整数对（a，b）：存在x0，使得f（x0）是f（x）的最大值，g（x0）是g（x）的最小值；
（3）对满足（2）中的条件的整数对（a，b），试构造一个定义在D={x|x∈R且x≠2k，k∈Z}上的函数h（x），使h（x+2）=h（x），且当x∈（﹣2，0）时，h（x）=f（x）．
查看习题详情和答案>>
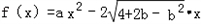，．（1）当b=0时，若f（x）在（﹣∞，2]上单调递减，求a的取值范围；
（2）求满足下列条件的所有整数对（a，b）：存在x0，使得f（x0）是f（x）的最大值，g（x0）是g（x）的最小值；
（3）对满足（2）中的条件的整数对（a，b），试构造一个定义在D={x|x∈R且x≠2k，k∈Z}上的函数h（x），使h（x+2）=h（x），且当x∈（﹣2，0）时，h（x）=f（x）．
，
．
，
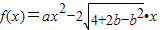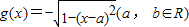时，求f（x）的反函数g（x）；
+t（x≥1）是“和谐函数”，求实数t的取值范围．