摘要： 教学对数运算性质及推导: ① 引例: 由.如何探讨和.之间的关系? 设, .由对数的定义可得:M=.N= ∴MN== ∴MN=p+q.即得MN=M + N ② 探讨:根据上面的证明.能否得出以下式子? 如果 a > 0.a ¹ 1.M > 0. N > 0 .则 ; , ① 讨论:自然语言如何叙述三条性质? 性质的证明思路?(运用转化思想.先通过假设.将对数式化成指数式.并利用幂运算性质进行恒等变形,然后再根据对数定义将指数式化成对数式) ④ 运用换底公式推导下列结论:,
网址：http://m.1010jiajiao.com/timu_id_4003337[举报]
在函数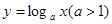
的图象上有
、
、
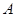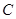三点，横坐标分别为
其中
．
⑴求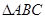
的面积
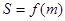的表达式；
⑵求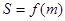的值域．
【解析】由题意利用分割可先表示三角形ABC的面积，然后应用对数运算性质及二次函数的性质求解函数的最大值，属于知识的简单综合.
查看习题详情和答案>>
教科书中有如下的对数运算性质：loga（MN）=logaM+logaN（a＞0，a≠1，M＞0，N＞0）．已知f（x）、g（x）互为反函数（x∈R），若函数g（x）有性质：对于任意的实数m，n，有g（mn）=g（m）+g（n），通过类比的思想，猜想函数f（x）性质：
查看习题详情和答案>>
对于任意的实数m，n，有f（m+n）=f（m）•f（n）
对于任意的实数m，n，有f（m+n）=f（m）•f（n）
．
下列各等式中，正确运用对数运算性质的是
A.lg(x2y
)=(lgx)2+lgy+
B.lg(x2y
)=(lgx)2+lgy+2lgz
C.lg(x2y
)=2lgx+lgy－2lgz D.lg(x2y
)=2lgx+lgy+
lgz
lg[H
]，其中［H
摩尔／升，计算纯净水的pH．
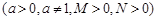．已知
、
互为反函数
，若函数
有性质：对于任意的实数
，有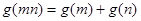
，通过类比的思想，猜想函数
性质：___________________________________________．