26、将连续的偶数2，4，6，8，10…排成以下的数表
（1）十字框一次框五个数，设中间的数为a，列式算出十字框中的五个数的和，你从中发现什么规律？
（2）若将十字框上、下、左、右平移，可框住另外五个数，这五个数还有上面规律吗？
（3）十字框中的五个数之和能等于2010吗？若能，请写出这五个数；若不能，说明理由．

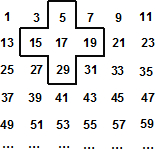将连续的奇数1，3，5，7，…，排成如下图的数表，用图中所示的十字框可任意框出5个数．
【探究规律一】：设十字框中间的奇数为a，则框中五个奇数之和用含a的代数式表示为．
【结论】：这说明能被十字框框中的五个奇数之和一定是自然数p的奇数倍，这个自然数p是．
【探究规律二】：落在十字框中间且又是第二列的奇数是15，27，39，51…则这一列数可以用代数式表示为12m+3（m为正整数），同样，落在十字框中间且又是第三列，第四列的奇数分别可表示为．
【运用规律】：
（1）已知被十字框框中的五个奇数之和为6025，则十字框中间的奇数是；这个奇数落在从左往右第列．
（2）被十字框框中的五个奇数之和可能是485吗？可能是3045吗？说说你的理由．

如图，将连续奇数1、3、5、7、9、……排成数阵，有一个能够在数阵中上下左右平移的十字框，当它能够恰好盖住此数阵中的五个数时，称其为标准十字框（如图中的阴影部分）

射雕英雄传中，英姑对黄蓉说：“你算法自然精我百倍，可是我问你：将一至九个数字排成三列，不论纵横斜角，每三个字相加都是十五，如何排列？”黄蓉当下低声诵到：“九宫之意，法以灵龟，二四为肩，六八为足，左三右七，戴九覆一，五居中央，…”请按黄蓉所述将一至九这九个数字填在宫中．