摘要：灵活运用绝对值不等式两个重要性质定理.特别关注等号成立的条件. 同步练习 6.6含绝对值的不等式 [选择题]
网址：http://m.1010jiajiao.com/timu_id_3999981[举报]
解不等式：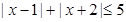 
【解析】本试题主要是考查了分段函数与绝对值不等式的综合运用。利用零点分段论 的思想，分为三种情况韬略得到解集即可。也可以利用分段函数图像来解得。
解：方法一：零点分段讨论：
方法二：数形结合法：
查看习题详情和答案>>
（2006•宝山区二模）给出函数f(x)=
+tx（x∈R）．
（1）当t≤-1时，证明y=f（x）是单调递减函数；
（2）当t=
时，可以将f（x）化成f(x)=a(
+x)+b(
-x)的形式，运用基本不等式求f（x）的最小值及此时x的取值；
（3）设一元二次函数g（x）的图象均在x轴上方，h（x）是一元一次函数，记F(x)=
+h(x)，利用基本不等式研究函数F（x）的最值问题．
查看习题详情和答案>>
| x2+4 |
（1）当t≤-1时，证明y=f（x）是单调递减函数；
（2）当t=
| 1 |
| 2 |
| x2+4 |
| x2+4 |
（3）设一元二次函数g（x）的图象均在x轴上方，h（x）是一元一次函数，记F(x)=
| g(x) |
>0},则A∩B等于