摘要:含绝对值不等式的证明.要善于应用分析转化法
网址:http://m.1010jiajiao.com/timu_id_3999980[举报]
已知函数 =
= .
.
(Ⅰ)当 时,求不等式
时,求不等式
 ≥3的解集;
≥3的解集;
(Ⅱ) 若 ≤
≤ 的解集包含
的解集包含 ,求
,求 的取值范围.
的取值范围.
【命题意图】本题主要考查含绝对值不等式的解法,是简单题.
【解析】(Ⅰ)当 时,
时, =
= ,
,
当 ≤2时,由
≤2时,由 ≥3得
≥3得 ,解得
,解得 ≤1;
≤1;
当2< <3时,
<3时, ≥3,无解;
≥3,无解;
当 ≥3时,由
≥3时,由 ≥3得
≥3得 ≥3,解得
≥3,解得 ≥8,
≥8,
∴ ≥3的解集为{
≥3的解集为{ |
| ≤1或
≤1或 ≥8};
≥8};
(Ⅱ)  ≤
≤
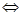
 ,
,
当 ∈[1,2]时,
∈[1,2]时, =
= =2,
=2,
∴ ,有条件得
,有条件得 且
且 ,即
,即 ,
,
故满足条件的 的取值范围为[-3,0]
的取值范围为[-3,0]
查看习题详情和答案>>
设A={x||x-1|<2},B={x|![]() >0},则A∩B等于
>0},则A∩B等于
A.{x|-1<x<3} B.{x|x<0或x>2}
C.{x|-1<x<0} D.{x|-1<x<0或2<x<3}
本题考查含绝对值不等式、分式不等式的解法及集合的运算.在进行集合运算时,把解集标在数轴上,借助图形可直观求解.
查看习题详情和答案>>